题目内容
11.如图是一块学生用直角三角板,其中∠A′=30°,三角板的边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等).将直径为4cm的⊙O移向三角板,三角板的内△ABC的斜边AB恰好等于⊙O的直径,它的外△A′B′C′的直角边A′C′恰好与⊙O相切(如图2),则边B′C′的长为3+$\sqrt{3}$cm.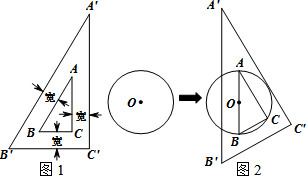
分析 设直线AC交A′B′于M,交B′C′于N,过A点作AH⊥A′B′于H,则有∠AMH=30°,AH=1,得到AM=2AH=2,可计算出MN=AM+AC+CN=3+2$\sqrt{3}$,在Rt△MB′N中利用含30°的直角三角形三边的关系得到B′N=$\frac{1}{\sqrt{3}}$NM=$\sqrt{3}$+2,则B′C′=B′N+NC′=$\sqrt{3}$+3.
解答 解:设直线AC交A′B′于M,交B′C′于N,过A点作AH⊥A′B′于H,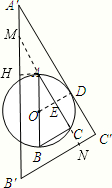
∵内、外直角三角形对应边互相平行且三处所示宽度相等,
∴∠AMH=30°,AH=1,
AM=2AH=2,
∴MN=AM+AC+CN=3+2$\sqrt{3}$,
在Rt△MB′N中,
∵∠B′MN=30°,
∴B′N=$\frac{1}{\sqrt{3}}$NM=$\sqrt{3}$+2,
∴B′C′=B′N+NC′=$\sqrt{3}$+3,
故答案为:3+$\sqrt{3}$.
点评 本题主要考查了切线的性质,含30°直角三角形的性质,以及平行线的性质,当直线与圆相切时,圆心到切线的距离等于圆的半径,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
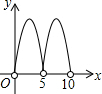
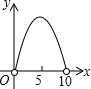
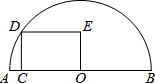 如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )
如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )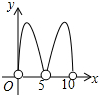
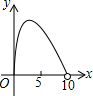
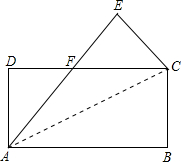 已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,
已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,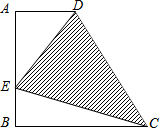 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问: 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息回答下列问题:
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息回答下列问题: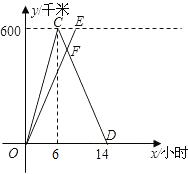 已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象. 如图,画出四边形ABCD关于点O的对称图形.
如图,画出四边形ABCD关于点O的对称图形.