题目内容
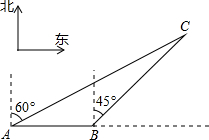 如图:我渔政310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
如图:我渔政310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)考点:解直角三角形的应用-方向角问题
专题:几何图形问题
分析:首先作CD⊥AB,交AB的延长线于D,则当渔政310船航行到D处时,离渔政船C的距离最近,进而表示出AB的长,再利用速度不变得出等式求出即可.
解答: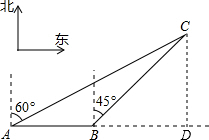 解:作CD⊥AB,交AB的延长线于D,则当渔政310船航行到D处时,离渔政船C的距离最近,
解:作CD⊥AB,交AB的延长线于D,则当渔政310船航行到D处时,离渔政船C的距离最近,
设CD长为x,
在Rt△ACD中,
∵∠ACD=60°,tan∠ACD=
,
∴AD=
x,
在Rt△BCD中,∵∠CBD=∠BCD=45°,
∴BD=CD=x,
∴AB=AD-BD=
x-x=(
-1)x,
设渔政船从B航行到D需要t小时,则
=
,
∴
=
,
∴(
-1)t=0.5,
解得:t=
,
∴t=
,
答:渔政310船再按原航向航行
小时后,离渔船C的距离最近.
 解:作CD⊥AB,交AB的延长线于D,则当渔政310船航行到D处时,离渔政船C的距离最近,
解:作CD⊥AB,交AB的延长线于D,则当渔政310船航行到D处时,离渔政船C的距离最近,设CD长为x,
在Rt△ACD中,
∵∠ACD=60°,tan∠ACD=
| AD |
| CD |
∴AD=
| 3 |
在Rt△BCD中,∵∠CBD=∠BCD=45°,
∴BD=CD=x,
∴AB=AD-BD=
| 3 |
| 3 |
设渔政船从B航行到D需要t小时,则
| AB |
| 0.5 |
| BD |
| t |
∴
(
| ||
| 0.5 |
| x |
| t |
∴(
| 3 |
解得:t=
| 0.5 | ||
|
∴t=
| ||
| 4 |
答:渔政310船再按原航向航行
| ||
| 4 |
点评:此题主要考查了方向角问题以及锐角三角函数关系等知识,利用渔政船速度不变得出等式是解题关键.

练习册系列答案
相关题目

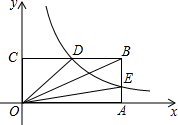 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=