题目内容
11.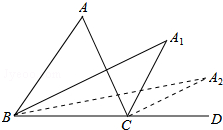 如图,在△ABC中,∠A=80,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2015BC的平分线与∠A2015CD的平分线交于点A2016,得∠A2016CD,则∠A2016=( )
如图,在△ABC中,∠A=80,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2015BC的平分线与∠A2015CD的平分线交于点A2016,得∠A2016CD,则∠A2016=( )| A. | 80•2-2014 | B. | 80•2-2015 | C. | 80•2-2016 | D. | 80•2-2017 |
分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,然后整理得到∠A1=$\frac{1}{2}$∠A,同理可得∠A2=$\frac{1}{2}$∠A1,从而判断出后一个角是前一个角的$\frac{1}{2}$,然后表示出,∠An即可.
解答 解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
∴∠A1+∠A1BC=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠A1BC,
∴∠A1=$\frac{1}{2}$∠A,
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{80}{4}$,
…,
∠An=$\frac{80}{{2}^{n}}$.
所以∠A2016=$\frac{80}{{2}^{2016}}$=80•2-2016.
故选:C.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的$\frac{1}{2}$是解题的关键.

练习册系列答案
相关题目
1.过多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形的内角和等于( )
| A. | 900° | B. | 1260° | C. | 1440° | D. | 1800° |
16. 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )| A. | 中位数是6.5 | |
| B. | 平均数高于众数 | |
| C. | 极差为3 | |
| D. | 平均每周锻炼超过6小时的人占总数的一半 |
20.下列命题中,是真命题的是( )
①正三角形都相似;②含45°的直角三角形都相似; ③含30°的直角三角形都相似; ④直角三角形斜边上的高分原三角形成的两个小三角形相似;⑤菱形都相似;⑥矩形都相似;⑦正方形都相似;⑧圆形都相似.
①正三角形都相似;②含45°的直角三角形都相似; ③含30°的直角三角形都相似; ④直角三角形斜边上的高分原三角形成的两个小三角形相似;⑤菱形都相似;⑥矩形都相似;⑦正方形都相似;⑧圆形都相似.
| A. | ①②③④⑦⑧ | B. | ①②③⑦⑧ | C. | ②③⑥⑦⑧ | D. | ①④⑤⑦⑧ |
 如图,AC,BD相交于点O,AB∥CD,AD∥BC,E,F分别是OB,OD的中点,求证:四边形AFCE是平行四边形.
如图,AC,BD相交于点O,AB∥CD,AD∥BC,E,F分别是OB,OD的中点,求证:四边形AFCE是平行四边形. 请把下面的小船图案先向上平移3格,再向右平移4格,最后为这个图案配上一句简短的解说词.
请把下面的小船图案先向上平移3格,再向右平移4格,最后为这个图案配上一句简短的解说词.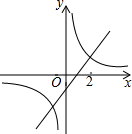 如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).
如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).