题目内容
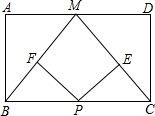 如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.
如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.考点:正方形的判定,矩形的性质
专题:
分析:根据矩形的性质和已知条件推出∠A=∠D=90°,AB=CD,AM=DM,求出∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,求出∠BMC=90°,即可求出矩形PEMF.根据AAS证△BFP≌△CEP,推出PE=PF即可.
解答:解:当P是BC的中点时,四边形PEMF为正方形.理由如下:
∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵AD=2AB=2CD,AM=DM=
AD,
∴AB=AM=DM=CD,
∴∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,
∴∠BMC=180°-45°-45°=90°,
∵PE⊥MC,PF⊥BM,
∴∠MEP=∠FPE=90°,
∴四边形PEMF为矩形,
∴∠PFM=∠PFB=∠PEC=90°.
在△BFP和△CEP中
,
∴△BFP≌△CEP(AAS),
∴PE=PF,
∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当P是BC的中点时,矩形PEMF为正方形.
∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵AD=2AB=2CD,AM=DM=
| 1 |
| 2 |
∴AB=AM=DM=CD,
∴∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,
∴∠BMC=180°-45°-45°=90°,
∵PE⊥MC,PF⊥BM,
∴∠MEP=∠FPE=90°,
∴四边形PEMF为矩形,
∴∠PFM=∠PFB=∠PEC=90°.
在△BFP和△CEP中
|
∴△BFP≌△CEP(AAS),
∴PE=PF,
∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当P是BC的中点时,矩形PEMF为正方形.
点评:本题主要考查对矩形的判定和性质,正方形的判定,等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
用长4米的铝材制成一个矩形窗框,使它的面积为0.75米2.若设它的一边长为x米,根据题意列出关于x的方程为( )
| A、x(2-x)=0.75 |
| B、2x(2-x)=0.75 |
| C、x(4-2x)=0.75 |
| D、x(4-x)=0.75 |
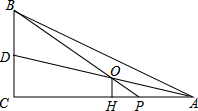 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?
如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?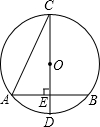 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2