题目内容
7.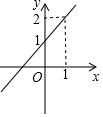 已知:一次函数的图象如图所示.
已知:一次函数的图象如图所示.(1)求直线l的解析式;
(2)求函数的图象与两坐标轴的交点坐标;
(3)求函数的图象与两坐标轴所围成的三角形的面积.
分析 (1)设解析式为:y=kx+b,把(0,1)和(1,2)代入列方程组解出即可;
(2)把x=0和y=0代入计算;
(3)计算直角△AOB的面积.
解答  解:(1)设直线l的解析式为:y=kx+b,
解:(1)设直线l的解析式为:y=kx+b,
把(0,1)和(1,2)代入得:$\left\{\begin{array}{l}{k+b=2}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线l的解析式为:y=x+1,
(2)当x=0时,y=1,
当y=0时,x=-1,
∴与x轴交点A的坐标为(-1,0),与y轴交点B的坐标为(0,1),
(3)∵A(-1,0),B(0,1),
∴OA=1,OB=1,
∴S△AOB=$\frac{1}{2}$×OA×OB=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
则函数的图象与两坐标轴所围成的三角形的面积为$\frac{1}{2}$.
点评 本题考查了利用待定系数法求一次函数的解析式及两坐标轴的交点坐标,属于常考题型,难度不大,解题思路为:①设解析式,②找直线上的两点坐标代入列方程组,③解方程组.

练习册系列答案
相关题目

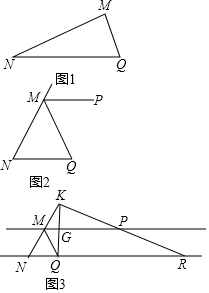 在三角形MNQ中.
在三角形MNQ中.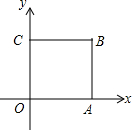 如图,在平面直角坐标系xOy中,边长为2的正方形OCBA,点A、C分别在x轴、y轴上,把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1( 0<α<90)﹒
如图,在平面直角坐标系xOy中,边长为2的正方形OCBA,点A、C分别在x轴、y轴上,把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1( 0<α<90)﹒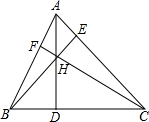 如图,AD为锐角△ABC的高线(AC>AB),H为线段AD上一点,连结BH,CH并延长分别交三角形的边于点E,F,且∠ABE=∠ACF,求证:H为△ABC的垂心.
如图,AD为锐角△ABC的高线(AC>AB),H为线段AD上一点,连结BH,CH并延长分别交三角形的边于点E,F,且∠ABE=∠ACF,求证:H为△ABC的垂心. 如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=17度.
如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=17度.