题目内容
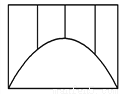
如图，一座抛物线型拱桥，桥下水面宽度是4m时，拱高为2m，一艘木船宽2m.要能顺利从桥下通过，船顶点与桥拱之间的间隔应不少于0.3m，那么木船的高不得超过 ______m.
1.2
【解析】以水面所在水平线为x轴，过拱桥顶点作水平线的垂线，作为y轴，建立坐标系，设水平面与拱桥的交点为A（-2，0），B（2，0），C（0，2），利用待定系数法设函数的解析式为y=a（x+2）（x-2）代入点C坐标，求得a=-，即抛物线的解析式为y=-（x+2）（x-2），令x=1，解得y=1.5，船顶与桥拱之间的间隔应不少于0.3，则木船的最高高度为1.5-0.3=1.2米.
...
若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）
A. 7 B. 10 C. 35 D. 70
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式，即可得出关于n的一元一次方程，解方程即可求出n的值，将其代入中即可得出结论．
【解析】
∵一个正n边形的每个内角为144°，
∴144n=180×（n﹣2），解得：n=10．
这个正n边形的所有对角线的条数是：==35．
故选C． 已知二次函数y＝x2－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x2－3x＋m＝0的两实数根是( )
A. x1＝1，x2＝－1 B. x1＝1，x2＝2 C. x1＝1，x2＝0 D. x1＝1，x2＝3
B
【解析】试题分析：关于x的一元二次方程x2-3x+m=0的两实数根就是二次函数y=x2-3x+m（m为常数）的图象与x轴的两个交点的横坐标．∵二次函数的解析式是y=x2-3x+m（m为常数），∴该抛物线的对称轴是：x=．
又∵二次函数y=x2-3x+m（m为常数）的图象与x轴的一个交点为（1，0），
∴根据抛物线的对称性质知，该抛物线与x轴的另一个交点的坐标是（2，0），
... 如图所示为一个污水净化塔内部，污水从上方入口进入后，流经形如等腰直角三角形的净化材枓表面，流向如图中箭头所示，每一次水流流经三角形两腰的机会相同，经过四层净化后流入底部的5个出口中的一个．下列判断：①5个出口的出水量相同；②2号出口的出水量与4号出口的出水量相同；③1，2，3号出水口的出水量之比约为1：4：6；④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．其中正确的判断有（ ）个．
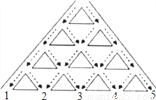
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】根据出水量假设出第一次分流都为1，可以得出下一次分流的水量，依此类推得出最后得出每个出水管的出水量，进而得出答案．
【解析】
根据图示可以得出：
①根据图示出水口之间存在不同，故此选项错误；
②2号出口的出水量与4号出口的出水量相同；
根据第二个出水口的出水量为： +=，
第4个出水口的出水量为： +=，
故此选项正确；
③1，2，3号... 如图，从A地到C地，可供选择的方案是走水路、走陆路、走空中，从A地到B地有两条水路、两条陆路，从B地到C地有3条陆路可供选择，走空中，从A地不经B地直线到C地，则从A地到C地可供选择的方案有（ ）
A. 20种 B. 8种 C. 5种 D. 13种
D
【解析】此题只需分别数出A到B、B到C、A到C的条数，再进一步分析计算即可．
【解析】
观察图形，得
A到B有4条，B到C有3条，所以A到B到C有4×3=12条，A到C一条．
所以从A地到C地可供选择的方案共13条．
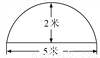
故选D． 如图为某菜农搭建的一个横截面为抛物线的大棚，有关尺寸如图所示，某菜农身高1.6米，则他在不弯腰的情况下在大棚内左右活动的范围是( )
A.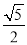 
米 B.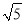 
米 C. 1.6米 D. 0.8米
B
【解析】如图，设抛物线的解析式为y=a（x-2.5）2+2，由待定系数法求出抛物线的解析式y=- （x-2.5）2+2，将y=1.6时代入解析式得- （x-2.5）2+2=1.6，解得， ，他在不弯腰的情况下在大棚里活动的范围是：x1-x2=．
故选：B. 在边长为1个单位长度的小正方形组成的网格中，点A、B、C、O都是格点．
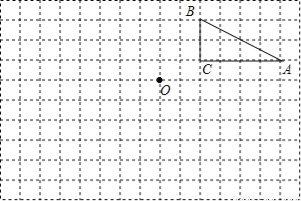
（1）将△ABC向左平移6个单位得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
（1）作图见解析；（2）作图见解析.
【解析】试题分析：（1）把A、B、C三点分别向左平移6个单位长度，即可得到三个顶点的对应点，然后顺次连接三点即可；
（2）连接AO并延长，然后截取OA2=OA，则A2就是A的对应点，同样可以作出B、C的对应点，然后顺次连接即可．
【解析】
（1）所作图形如图所示；
（2）所作图形如图所示． 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
B
【解析】试题解析：A、不是中心对称图形，本选项错误；
B、是中心对称图形，本选项正确；
C、不是中心对称图形，本选项错误；
D、不是中心对称图形，本选项错误．
故选B． 已知：如图，△ABC的∠B、∠C的平分线相交于点D，过D作MN∥BC交AB、AC分别于点M、N，求证：BM＋CN＝MN.
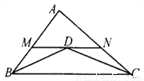
见解析
【解析】试题分析：根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠6=∠2，∠3=∠5，然后求出∠1=∠6，∠4=∠5，根据等角对等边的性质可得BM=DM，CN=DN，然后列式求解即可得证．
试题解析：证明：
∵BD、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠3=∠4，
∵MN∥BC，
∴∠6=∠2，∠3=∠5，
...