题目内容
14.(1)如图1,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的角平分线,试探究∠BPC与∠A的关系.(2)如图2,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠E与∠A的关系.
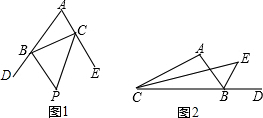
分析 (1)根据三角形外角平分线的性质可得∠BCP=$\frac{1}{2}$(∠A+∠ABC)、∠PBC=$\frac{1}{2}$(∠A+∠ACB);根据三角形内角和定理可得∠BPC=90°-$\frac{1}{2}$∠A;
(2)根据CE为∠ABC的角平分线,BE为△ABC外角∠ABD的平分线,可知,∠A=180°-∠1-∠3,∠E=180°-∠4-∠ABE=180°-∠3-$\frac{1}{2}$(∠A+2∠1),两式联立可得2∠BEC=∠A.
解答 (1)∠BPC=90°-$\frac{1}{2}$∠A.
证明:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°
∴∠BCP=$\frac{1}{2}$(∠A+∠ABC)、∠PBC=$\frac{1}{2}$(∠A+∠ACB),
由三角形内角和定理得,∠BPC=180°-∠BCP-∠PBC,
=180°-$\frac{1}{2}$[∠A+(∠A+∠ABC+∠ACB)],
=180°-$\frac{1}{2}$(∠A+180°),
=90°-$\frac{1}{2}$∠A;
(2)2∠BEC=∠A.
证明:如图,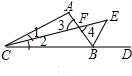
∵CE为∠ACB的角平分线,BE为△ABC外角∠ABD的平分线,两角平分线交于点E,
∴∠1=∠2,∠ABE=$\frac{1}{2}$(∠A+2∠1),∠3=∠4,
在△ACF中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A----①
在△BEF中,∠E=180°-∠4-∠ABE=180°-∠3-$\frac{1}{2}$(∠A+2∠1),
即2∠E=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,
把①代入②得2∠E=∠A,即2∠BEC=∠A.
点评 本题考查的是三角形内角和定理,涉及到三角形内角与外角的关系,角平分线的性质,掌握三角形的内角和180°是解决问题的关键.

| A. | 正方形 | B. | 长方形 | C. | 梯形 | D. | 直角三角形 |
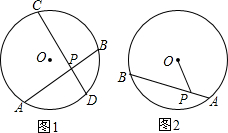
 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.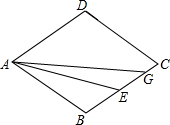 如图,在菱形ABCD中,点E为BC的中点,点G在BC边上,连结AE,AG.
如图,在菱形ABCD中,点E为BC的中点,点G在BC边上,连结AE,AG.
 如图,AB⊥DB,CD⊥DB,∠1=∠2.射线BE与DF是否平行?请说明理由.
如图,AB⊥DB,CD⊥DB,∠1=∠2.射线BE与DF是否平行?请说明理由.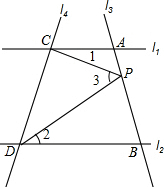 如图,已知直线l1∥l2,且l3和l1,l2分别交于A、B两点,l4与l1,l2分别交于C、D两点,点P在直线AB上,且在l4的右侧.
如图,已知直线l1∥l2,且l3和l1,l2分别交于A、B两点,l4与l1,l2分别交于C、D两点,点P在直线AB上,且在l4的右侧.