题目内容
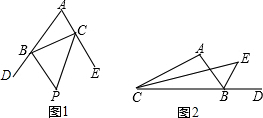
4.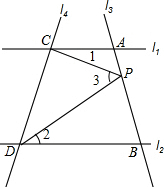 如图,已知直线l1∥l2,且l3和l1,l2分别交于A、B两点,l4与l1,l2分别交于C、D两点,点P在直线AB上,且在l4的右侧.
如图,已知直线l1∥l2,且l3和l1,l2分别交于A、B两点,l4与l1,l2分别交于C、D两点,点P在直线AB上,且在l4的右侧.(1)如图,试猜想:∠1,∠2,∠CPD之间的关系;
(2)如果点P在A、B两点之间运动时,∠1,∠2,∠CPD之间的关系是否发生变化?(只说结论,不要求证明)
(3)如果点P在A、B两点的外侧运动时,试探究∠1,∠2,∠CPD之间的关系.
(点P和A、B不重合),并加以证明.
分析 (1)根据图形作出猜想即可;
(2)作PE∥AC,如图1,由于l1∥l2,则PE∥BD,根据平行线的性质得∠1=∠EPC,∠2=∠EPD,所以∠1+∠2=∠3;
(3)分当P点在A的外侧与当P点在B的外侧两种情况进行分类讨论即可.
解答 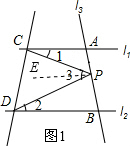 解:(1)猜想:∠CPD=∠1+∠2;
解:(1)猜想:∠CPD=∠1+∠2;
(2)∠1,∠2,∠CPD之间的关系不发生变化
仍是:∠CPD=∠1+∠2;
作PE∥AC,如图1,
∵l1∥l2,
∴PE∥BD,
∴∠1=∠EPC,∠2=∠EPD,
∴∠1+∠2=∠3,即∠CPD=∠1+∠2;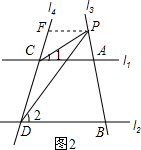
(3)当P点在A的外侧时,如图a,过P作PF∥l1,交l4于F,
∴∠1=∠FPC.
∵l1∥l4,
∴PF∥l2,
∴∠2=∠FPD
∵∠CPD=∠FPD-∠FPC
∴∠CPD=∠2-∠1.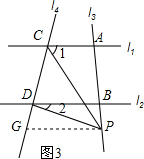
当P点在B的外侧时,如图b,过P作PG∥l2,交l4于G,
∴∠2=∠GPD
∵l1∥l2,
∴PG∥l1,
∴∠1=∠CPG
∵∠CPD=∠CPG-∠GPD
∴∠CPD=∠1-∠2.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若一元二次方程ax2+bx+c=0中的二次项系数、一次项系数与常数项之和等于零,那么方程必有一个根是( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
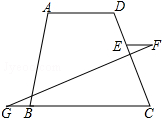 已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?
已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?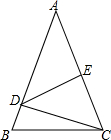 如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△BDC的周长为13cm,则△ABC的周长为19.
如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△BDC的周长为13cm,则△ABC的周长为19.