题目内容
10.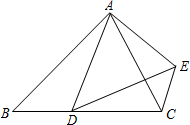 已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.
已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.(1)求证:△BAC∽△DAE;
(2)当∠BAC=90°时,求证:EC⊥BC.
分析 (1)由∠BAD=∠CAE可得∠DAE,由$\frac{AD}{AB}$=$\frac{AE}{AC}$得到$\frac{AB}{AD}$=$\frac{AC}{AE}$,则根据相似三角形的判定方法可得△BAC∽△DAE;
(2)根据相似三角形的性质,由△BAC∽△DAE得到∠B=∠ACE,再由三角形内角和得到∠B+∠ACB=90°,所以∠ACB+∠ACB=90°,于是可判断EC⊥BC.
解答 (1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,即∠DAE,
∵$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,
∴△BAC∽△DAE;
(2)解:∵△BAC∽△DAE,
∴∠B=∠ACE,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠ACB=90°,即∠BCE=90°,
∴EC⊥BC.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时主要利用相似比计算相应线段的长和得到对应角相等.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.下列计算中正确的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | ${(\frac{1}{2}x+5)^2}=\frac{1}{4}{x^2}+5x+25$ |
19.方程x2=x的解为( )
| A. | x=0 | B. | x=1 | C. | x1=0,x2=1 | D. | x1=0,x2=-1 |
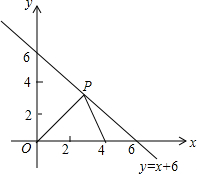 如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=6-x上一点,O是坐标原点.
如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=6-x上一点,O是坐标原点.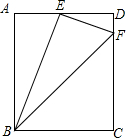 如图,在矩形ABCD中,E是AD的中点,F是CD的上一点,FE⊥BE.
如图,在矩形ABCD中,E是AD的中点,F是CD的上一点,FE⊥BE. 如图,AD∥BC∥EF,AE:AB=2:3,DF=8,则FC=4.
如图,AD∥BC∥EF,AE:AB=2:3,DF=8,则FC=4.