题目内容
20.在平面直角坐标系xOy中,已知点A(1,$\sqrt{3}$),在坐标轴上找一点P,使得△AOP是等腰三角形,则符合条件的点P的个数为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 ①AO垂直平分线与两坐标轴有2个交点;②以A为圆心,AO长为半径画圆,与两坐标轴有2个交点;③以O为圆心,AO长为半径画圆,与两坐标轴有4个交点.
解答  解:如图所示:
解:如图所示:
①AO垂直平分线与两坐标轴有2个交点;
②以A为圆心,AO长为半径画圆,与两坐标轴有2个交点;
③以O为圆心,AO长为半径画圆,与两坐标轴有4个交点,
共有2+2+4=8个交点,
因为点A坐标(1,$\sqrt{3}$),所以∠AOP1=60°,△AOP1是等边三角形,
所以P1、P6、P8重合,
所以共有6个点.
故选B.
点评 本题考查了等腰三角形的判定及坐标与图形的性质;针对线段OA在等腰三角形中的地位,分类讨论用画圆弧的方式,找与坐标轴的交点,比较形象易懂.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
15.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:$\overline{x_甲}$=9环,$\overline{x_乙}$=9环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
| 甲 | 10 | 9 | 8 | 8 | 10 | 9 |
| 乙 | 10 | 10 | 8 | 10 | 7 | 9 |
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
5.已知直线$y=\frac{1}{2}x+5$与一条经过原点的直线l平行,则这条直线l的函数关系式为( )
| A. | $y=-\frac{1}{2}x+5$ | B. | $y=\frac{1}{2}x$ | C. | $y=-\frac{1}{2}x$ | D. | y=2x |
12.“社会主义核心价值观”要求我们牢记心间,小明在“百度”搜索“社会主义核心价值观”,找到相关结果约为4280000个,数据4280000用科学记数法表示为( )
| A. | 0.428×107 | B. | 4.28×106 | C. | 4.28×105 | D. | 428×104 |
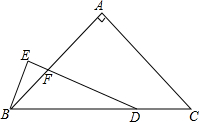 如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.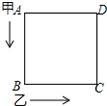 如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.
如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.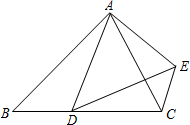 已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.
已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.