题目内容
1.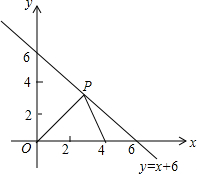 如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=6-x上一点,O是坐标原点.
如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=6-x上一点,O是坐标原点.(1)设P(x,y),求△OPA的面积S与x的函数解析式;
(2)当S=10时,求P点的坐标;
(3)在直线上y=6-x求一点P,使△POA是以OA为底边的等腰三角形.
分析 (1)过P作PB垂直于x轴,把P坐标代入直线y=6-x,表示出y,进而表示出PB,由A的坐标确定出OA的长,确定出△OPA的面积S与x的函数解析式即可;
(2)把S=10代入S与x的函数解析式,求出x的值,即可确定出此时P的坐标;
(3)作线段OA的垂直平分线,交直线y=6-x于点P,连接OP,AP,△POA是以OA为底边的等腰三角形,把x=2代入直线y=6-x求出y的值,即可求出此时P的坐标.
解答 解:(1)过P作PB⊥x轴,交x轴于点B,如图1所示,
∵P(x,y),且P在直线y=6-x上,
∴y=6-x,即P(x,6-x),
∴PB=6-x,
∵A(4,0),
∴OA=4,
∴△OPA的面积S与x的函数解析式为S=$\frac{1}{2}$OA•PB=2(6-x)=12-2x;
(2)当S=10时,12-2x=10,
解得:x=1,
此时P坐标为(1,5);
(3)作线段OA的垂直平分线,交直线y=6-x于点P,连接OP,AP,如图2所示,△POA是以OA为底边的等腰三角形,
把x=2代入直线y=6-x得:y=6-2=4,此时P坐标为(2,4).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,三角形的面积求法,等腰三角形的性质,熟练掌握一次函数的性质是解本题的关键.

练习册系列答案
相关题目
12.“社会主义核心价值观”要求我们牢记心间,小明在“百度”搜索“社会主义核心价值观”,找到相关结果约为4280000个,数据4280000用科学记数法表示为( )
| A. | 0.428×107 | B. | 4.28×106 | C. | 4.28×105 | D. | 428×104 |
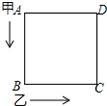 如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.
如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.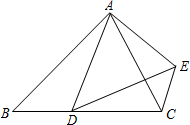 已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.
已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.