题目内容
18.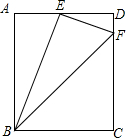 如图,在矩形ABCD中,E是AD的中点,F是CD的上一点,FE⊥BE.
如图,在矩形ABCD中,E是AD的中点,F是CD的上一点,FE⊥BE.(1)求证:△ABE与△BEF相似.
(2)若DE=3,AB=9.求sin∠CBF.
分析 (1)由FE⊥BE得到∠BEF=90°,则利用等角的余角相等得到∠ABE=∠DEF,则可证明△ABE∽△DEF,得到$\frac{BE}{EF}$=$\frac{AB}{DE}$,由于AE=DE,则$\frac{AB}{BE}$=$\frac{AE}{EF}$,加上∠A=∠BEF,于是可判断△ABE∽△EBF;
(2)由△ABE∽△DEF得到$\frac{AE}{DF}$=$\frac{AB}{DE}$,即$\frac{DF}{3}$=$\frac{9}{3}$,可计算出DF=1,所以CF=8,然后在Rt△BCF中,利用勾股定理可得到BF=10,然后根据正弦的定义求解.
解答 (1)证明:∵FE⊥BE,
∴∠BEF=90°,
∴∠AEB+∠DEF=90°,
而∠AEB+∠ABE=90°,
∴∠ABE=∠DEF,
而∠A=∠D,
∴△ABE∽△DEF,
∴$\frac{BE}{EF}$=$\frac{AB}{DE}$,
∵E是AD的中点,
∴AE=DE,
∴$\frac{AB}{AE}$=$\frac{BE}{EF}$,
即$\frac{AB}{BE}$=$\frac{AE}{EF}$,
∵∠A=∠BEF,
∴△ABE∽△EBF;
(2)解:∵△ABE∽△DEF,
∴$\frac{AE}{DF}$=$\frac{AB}{DE}$,即$\frac{DF}{3}$=$\frac{9}{3}$,
∴DF=1,
∵CD=AB=9,
∴CF=8,
在Rt△BCF中,
∵BC=AD=6,CF=8,
∴BF=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴sin∠CBF=$\frac{CF}{BF}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时主要利用相似比计算相应线段的长和得到对应角相等.解决(2)的关键是证明△ABE∽△DEF,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案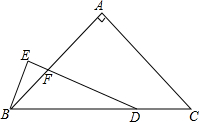 如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.
如图,在△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=$\frac{1}{2}$∠C,BE⊥DE于E,DE与AB交于点F,试探究线段BE与FD的数量关系,并证明.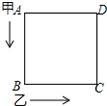 如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.
如图所示,甲乙两人同时出发沿着边长为90m的正方形,按A→B→C→D→A…的方向行走.甲从A点以66m/min的速度,乙从B点以72m/min的速度行走,当乙第一次追上甲时,用了45min.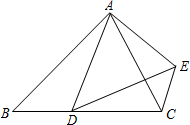 已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.
已知:如图,在△ABC中,点D为边BC上的点,$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠BAD=∠CAE.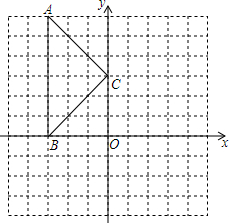 如图,将△ABC放于平面直角坐标系中,得到顶点坐标为A(-3,6),B(-3,0),C(0,3).以B为旋转中心,在平面直角坐标系内将△ABC顺时针旋转90°.
如图,将△ABC放于平面直角坐标系中,得到顶点坐标为A(-3,6),B(-3,0),C(0,3).以B为旋转中心,在平面直角坐标系内将△ABC顺时针旋转90°.