题目内容
 在平面直角坐标系中,以原点O为圆心的圆过点A(0,3
在平面直角坐标系中,以原点O为圆心的圆过点A(0,3| 5 |
考点:垂径定理,坐标与图形性质,勾股定理
专题:
分析:连接OB,过点O作OD⊥BC于点D,根据直线y=kx-3k+4必过点D(3,4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(0,3
),求出OB的长,再利用勾股定理求出BD,即可得出答案.
| 5 |
解答: 解:连接OB,过点O作OD⊥BC于点D,
解:连接OB,过点O作OD⊥BC于点D,
∵直线y=kx-3k+4必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(0,3
),
∴圆的半径为3
,
∴OB=3
,
∴BD=
=2
,
∴BC的长的最小值为4
;
故答案为:4
.
 解:连接OB,过点O作OD⊥BC于点D,
解:连接OB,过点O作OD⊥BC于点D,∵直线y=kx-3k+4必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(0,3
| 5 |
∴圆的半径为3
| 5 |
∴OB=3
| 5 |
∴BD=
| 20 |
| 5 |
∴BC的长的最小值为4
| 5 |
故答案为:4
| 5 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 已知二次函数y=ax2+bx的图象如图所示,那么a、b的符号为( )
已知二次函数y=ax2+bx的图象如图所示,那么a、b的符号为( )| A、a>0,b>0; |
| B、a<0,b>0 |
| C、a>0,b<0 |
| D、a<0,b<0 |
代数式
的意义为( )
| x-y |
| 2 |
| A、x与y的一半的差 | ||
| B、x与y的差的一半 | ||
| C、x减去y除以2的差 | ||
D、x与y的
|
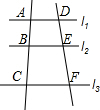 如图,直线l1∥l2∥l3,已知:AB=4,BC=6,DE=3,则EF=( )
如图,直线l1∥l2∥l3,已知:AB=4,BC=6,DE=3,则EF=( )| A、8 | B、6 | C、4.5 | D、2 |
关于x的一元二次方程-kx2-3x+5k=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定 |