题目内容
已知等边三角形的边长为6，则等边三角形的高为 ．
考点：等边三角形的性质
专题：
分析：如图，由等边三角形的边长为6，可得AB=AC=BC=6，∠B=60°，又由AD⊥BC，利用三角函数的知识（或勾股定理）即可求得AD的值．
解答：解：如图，
∵等边三角形的边长为6，
∴AB=AC=BC=6cm，∠B=60°，
∵AD⊥BC，
∴∠ADB=90°，
在Rt△ABD中，AD=AB•sin∠B=6×
=3
．
∴其高为3
．
故答案为：3
．
∵等边三角形的边长为6，
∴AB=AC=BC=6cm，∠B=60°，
∵AD⊥BC，
∴∠ADB=90°，
在Rt△ABD中，AD=AB•sin∠B=6×
| ||
| 2 |
| 3 |
∴其高为3
| 3 |
故答案为：3
| 3 |
点评：此题考查了等边三角形的性质以及三角函数的性质．此题比较简单，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
在平面直角坐标系中，以原点O为圆心的圆过点A（0，3
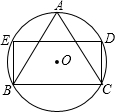如图，△ABC是⊙O的内接等边三角形，AB=1．点D，E在圆上，四边形BCDE为矩形，则这个矩形的面积是（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知a为非负数，比较2a与a的大小关系，正确的是（ ）
| A、2a≥a | B、2a≤a |
| C、2a＜a | D、2a＞a |
已知
=
，那么下列各等式一定成立的是（ ）
| a |
| b |
| c |
| d |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|