题目内容
在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点P(1,2),且与x轴正半轴交于点A,与y轴正半轴交于点B.若tan∠PAO=
,则点B的坐标是 .
| 1 |
| 2 |
考点:一次函数图象上点的坐标特征
专题:计算题
分析:根据一次函数图象上点的坐标特征得到k+b=2,再利用坐标轴上点的坐标特征得到B(0,b)、A(-
,0),接着利用正切的定义得到
=
,即
=
,解得k=-
,所以-
+b=2,解得b=
,于是可得到B点坐标.
| b |
| k |
| OB |
| OA |
| 1 |
| 2 |
| b | ||
-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:解: ∵一次函数y=kx+b的图象经过点P(1,2),
∵一次函数y=kx+b的图象经过点P(1,2),
∴k+b=2,
当x=0时,y=kx+b=b,则B(0,b);当y=0时,kx+b=0,解得x=-
,则A(-
,0),
∵tan∠PAO=
,即tan∠A=
,
∴
=
,即
=
,解得k=-
,
∴-
+b=2,
∴b=
.
故答案为(0,
).
 ∵一次函数y=kx+b的图象经过点P(1,2),
∵一次函数y=kx+b的图象经过点P(1,2),∴k+b=2,
当x=0时,y=kx+b=b,则B(0,b);当y=0时,kx+b=0,解得x=-
| b |
| k |
| b |
| k |
∵tan∠PAO=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| OB |
| OA |
| 1 |
| 2 |
| b | ||
-
|
| 1 |
| 2 |
| 1 |
| 2 |
∴-
| 1 |
| 2 |
∴b=
| 5 |
| 2 |
故答案为(0,
| 5 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.
| b |
| k |

练习册系列答案
相关题目
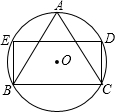 如图,△ABC是⊙O的内接等边三角形,AB=1.点D,E在圆上,四边形BCDE为矩形,则这个矩形的面积是( )
如图,△ABC是⊙O的内接等边三角形,AB=1.点D,E在圆上,四边形BCDE为矩形,则这个矩形的面积是( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知a为非负数,比较2a与a的大小关系,正确的是( )
| A、2a≥a | B、2a≤a |
| C、2a<a | D、2a>a |
 如图,开口向上的抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点坐标为(-1,0),则当y≥0时,x的取值范围是
如图,开口向上的抛物线y=ax2+bx+c的对称轴是直线x=1,与x轴的一个交点坐标为(-1,0),则当y≥0时,x的取值范围是 在平面直角坐标系中,以原点O为圆心的圆过点A(0,3
在平面直角坐标系中,以原点O为圆心的圆过点A(0,3