题目内容
1.在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.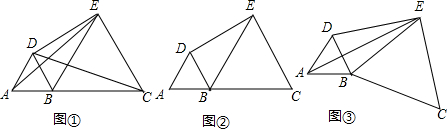
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求证:∠BDE=90°;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2,试求∠DEB的度数.
分析 (1)欲证明CD=AE,只要证明△ABE≌△DBC即可.
(2)如图②中,取BE中点F,连接DF,证出△DBF是等边三角形,进一步得出∴∠FDE=∠FED=30°,即可证明△BDE是直角三角形.
(3)如图③中,连接DC,先利用勾股定理的逆定理证明△DEC是直角三角形,得∠DEC=90°即可解决问题.
解答 (1)证明:∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,$\left\{\begin{array}{l}{AB=BD}&{\;}\\{∠ABE=∠DBC}&{\;}\\{BE=BC}&{\;}\end{array}\right.$,
∴△ABE≌△DBC(SAS),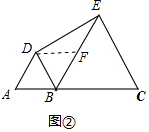
∴CD=AE.
(2)证明:如图②中,取BE中点F,连接DF.
∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,
∴BF=EF=1=BD,∠DBF=60°,
∴△DBF是等边三角形,
∴DF=BF=EF,∠DFB=60°,
∵∠BFD=∠FED+∠FDE,
∴∠FDE=∠FED=30°
∴∠EDB=180°-DEB∠DBE-∠DEB=90°.
(3)解:如图③中,连接DC,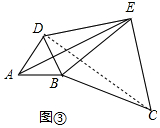
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,$\left\{\begin{array}{l}{AB=BD}&{\;}\\{∠ABE=∠DBC}&{\;}\\{BE=BC}&{\;}\end{array}\right.$,
∴△ABE≌△DBC(SAS),
∴AE=DC.
∵DE2+BE2=AE2,BE=CE,
∴DE2+CE2=CD2,
∴∠DEC=90°,
∵∠BEC=60°,
∴∠DEB=∠DEC-∠BEC=30°.
点评 本题考查全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识,寻找全等三角形是解决问题的关键,学会添加辅助线的方法,属于中考常考题型.

| A. | 3人 | B. | 4人 | C. | 5人 | D. | 6人 |
| A. | 80° | B. | 50° | C. | 80°或20° | D. | D20° |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | (x-$\frac{1}{2}$)2=$\frac{3}{4}$ | B. | (x+$\frac{1}{2}$)2=$\frac{3}{4}$ | C. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | D. | (x+$\frac{1}{2}$)2=$\frac{5}{4}$ |
| A. | m>1 | B. | m>-1 | C. | m<1 | D. | m<-1 |
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B($\frac{1}{2}$,y2),点C($\frac{5}{2}$,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B($\frac{1}{2}$,y2),点C($\frac{5}{2}$,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( ) 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE.
如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 如图:反比例函数y=$\frac{6}{x}$的图象如下,在图象上任取一点P,过P点作x轴的垂线交x轴于M,则三角形OMP的面积为( )
如图:反比例函数y=$\frac{6}{x}$的图象如下,在图象上任取一点P,过P点作x轴的垂线交x轴于M,则三角形OMP的面积为( )