题目内容
18.分解因式:x2y2-y2=y2(x+1)(x-1);
3a2-6a+3=3(a-1)2;
4a2+4a+1=(2a+1)2;
a-ab2=-a(b+1)(b-1);
(a2+b2)2-4a2b2=(a-b)4;
x2(a-b)2-y2(b-a)2=(a-b)2(x+y)(x-y);
(x2-4x)2+8(x2-4x)+16=(x-2)4.
分析 对于x2y2-y2,先提y2,然后利用平方差公式分解;
对于3a2-6a+3,先提3,然后利用完全平方公式分解;
对于4a2+4a+1,直接利用完全平方公式分解;
对于a-ab2,先提-a,然后利用平方差公式分解;
对于(a2+b2)2-4a2b2,先利用完全平方公式展开,然后利用完全平方公式分解;
对于x2(a-b)2-y2(b-a)2=,先提(a-b)2,然后利用平方差公式分解;
对于(x2-4x)2+8(x2-4x)+16,先把它看作关于x2-4x的二次三项式,然后利用完全平方公式分解.
解答 解:x2y2-y2=y2(x2-1)=y2(x+1)(x-1);
3a2-6a+3=3(a2-2a+1)=3(a-1)2;
4a2+4a+1=(2a+1)2;
a-ab2=-a(b2-1)=-a(b+1)(b-1);
(a2+b2)2-4a2b2=(a2-2ab+b2)2=(a-b)4;
x2(a-b)2-y2(b-a)2=(a-b)2(x2-y2)=(a-b)2(x+y)(x-y);
(x2-4x)2+8(x2-4x)+16=(x2-4x+4)2=(x-2)4.
故答案为y2(x+1)(x-1);3(a-1)2;(2a+1)2;-a(b+1)(b-1);(a-b)4;(a-b)2(x+y)(x-y); (x-2)4.
点评 本题考查了提公因式与公式法的综合运用:先提公因式,然后利用完全平方公式和平方差公式分解.

练习册系列答案
相关题目
3.据阿里巴巴官方数据显示,2016年中国“双11”淘宝天猫交易额为120 700 000 000元,将120 700 000 000元用科学记数法表示为( )元.
| A. | 0.1207×1011 | B. | 1.207×1010 | C. | 1.207×1011 | D. | 1207×108 |
 如图,△ABC≌△A'B'C',则∠B=100°.
如图,△ABC≌△A'B'C',则∠B=100°.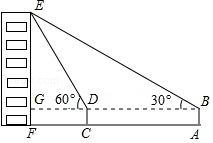 如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)
如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)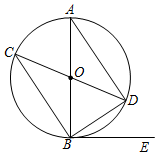 已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.