题目内容
13.某商场经营一批进价2元的小商品,在经营中发现此商品的日销售单价与日销量之间的关系如表:| 日销售单价(元) | 3 | 5 | 7 | 9 | 11 |
| 日销量(件) | 18 | 14 | 10 | 6 | 2 |
(2)如果用x表示日销售单价,y表示日销量,那么y与x之间的关系式是y=24-2x;
(3)日销售单价为7元时,商场日销售盈利最高?(盈利=日销售总额-日销售商品的总进价)
分析 (1)直接利用自变量以及因变量的关系得出答案;
(2)利用待定系数法求出一次函数解析式进而得出答案;
(3)首先得出盈利与售价的关系,进而利用二次函数最值求法得出答案.
解答 解:(1)由题意可得:日销售单价与日销量之间的关系,其中 日销售单价是自变量,日销量是因变量;
故答案为:日销售单价,日销量;
(2)由表格中数据可得y与x之间的关系式可设为:y=kx+b,
则$\left\{\begin{array}{l}{3k+b=18}\\{5k+b=14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=24}\end{array}\right.$,
故y与x之间的关系式是:y=24-2x;
故答案为:y=24-2x.
(3)由题意可得:w=(24-2x)(x-2)=-2x2+28x-48
当x=-$\frac{b}{2a}$=7时,w最大,故日销售单价为 7元时,商场日销售盈利最高.
故答案为:7.
点评 此题主要考查了函数关系式以及一次函数与二次函数的应用,正确得出函数关系式是解题关键.

练习册系列答案
相关题目
4.下列从左到右的变形,属于分解因式的是( )
| A. | (a-3)(a+3)=a2-9 | B. | x2+x-5=x(x+1)-5 | C. | a2+a=a(a+1) | D. | x3y=x•x2•y |
1.如图交通标志中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.富豪阁社区为了解居民每月用于信息消费的金额,随机抽取了部分家庭进行调查,数据整理成如图所示的不完整统计图,已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
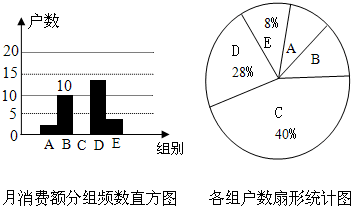
(1)A组的频数是2;本次调查样本的容量是50
(2)补全直方图(请标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
月消费额分组统计图

(1)A组的频数是2;本次调查样本的容量是50
(2)补全直方图(请标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
月消费额分组统计图
| 组别 | 消费额(元) |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
5. 如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
 如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )
如图,圆柱的底面半径是40,高为30π,一只蚂蚁在圆柱的侧面爬行,请问蚂蚁从点A爬到点B的最短路程是( )| A. | 50π | B. | 50 | C. | 500π | D. | 500 |
 如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为12cm.
如图,EF为△ABC的中位线,△AEF的周长为6cm,则△ABC的周长为12cm. 如图,在每个小正方形边长均为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长均为1的方格纸中,△ABC的顶点都在方格纸格点上.