题目内容
15.如果q>0,那么方程x2-px-q=0中,b2-4ac>0(填“>”或“<”)分析 将a=1,b=-p,c=-q代入b2-4ac,利用不等式的性质即可求解.
解答 解:∵a=1,b=-p,c=-q,
∴b2-4ac=(-p)2-4×1×(-q)=p2+4q,
∵q>0,
∴p2+4q>0,
∴b2-4ac>0.
故答案为>.
点评 本题主要考查了根的判别式:把△=b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
5.下列算式中,结果为正数的是( )
| A. | -(-4)2 | B. | -(-42) | C. | -|-4|2 | D. | -[-(-4)] |
10.若$\frac{a}{b}>0$,$\frac{c}{b}<0$,则ac( )
| A. | 大于0 | B. | 小于0 | C. | 不一定 | D. | 等于0 |
 实数a,b在数轴上的位置,如图所示,化简:$\sqrt{(a+b)^{2}}$+a+|b|=0.
实数a,b在数轴上的位置,如图所示,化简:$\sqrt{(a+b)^{2}}$+a+|b|=0.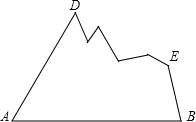 如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.
如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理. 如图,MN与PQ相交于点O,MP=MQ,NP=NQ,求证:OP=OQ,PQ⊥MN.
如图,MN与PQ相交于点O,MP=MQ,NP=NQ,求证:OP=OQ,PQ⊥MN.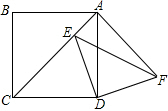 正方形ABCD边长为2$\sqrt{2}$,点E在对角线AC上,连接DE,将线段DE绕点D顺时针旋转90°至DF的位置,连接AF,EF.
正方形ABCD边长为2$\sqrt{2}$,点E在对角线AC上,连接DE,将线段DE绕点D顺时针旋转90°至DF的位置,连接AF,EF.