题目内容
3. 如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)
如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)
分析 先将图形展开,再根据两点之间线段最短,由勾股定理可得出.
解答 解:圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.
∵AB=π•$\frac{2}{π}$=2,CB=2.
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{13}$.
故答案为:$\sqrt{13}$
点评 此题主要考查了平面展开图最短路径问题,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各组数中,互为相反数的是 ( )
| A. | -2与$\root{3}{-8}$ | B. | -2与-$\sqrt{4}$ | C. | -2与-$\frac{1}{2}$ | D. | -2与$\root{3}{8}$ |
12.化简(2+1)(22+1)(24+1)(28+1)得( )
| A. | 28-1 | B. | 216+1 | C. | 216-1 | D. | 264-1 |
19.下列各式从左到右的变形中,是因式分解的是( )
| A. | (x+1)(x-2)=x2-x-2 | B. | x2-4+2x=(x+2)(x-2)+2x | ||
| C. | 2a(b+c)=2ab+2ac | D. | m2-n2=(m+n)(m-n) |
8.已知a-b=-2,那么-ax2+bx2化简的结果是( )
| A. | 2x2 | B. | -2x2 | C. | $\frac{1}{2}$x2 | D. | -$\frac{1}{2}$x2 |
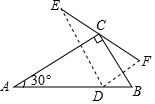 如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )
如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )