题目内容
16.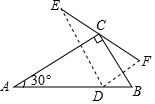 如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )
如图,在Rt△ABC中,AC=4,∠A=30°,点D在斜边AB上,点D关于AC、BC的对称点为E、F,则EF的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先连接CD,根据轴对称的性质,得出Rt△DEF中,CD=$\frac{1}{2}$EF,再根据垂线段最短,得出CD=$\frac{1}{2}$AC=2,最后根据直角三角形斜边上的中线性质,计算EF的最小值.
解答  解:连接CD,
解:连接CD,
∵点D关于AC、BC的对称点为E、F,
∴AC垂直平分DE,BC垂直平分DF,
∴CE=CD=CF,即C为EF的中点,
∵∠ACB=90°,
∴∠EDF=90°,
∴Rt△DEF中,CD=$\frac{1}{2}$EF,
∵点D在斜边AB上,
∴当CD⊥AB时,CD最短,
∵AC=4,∠A=30°,
∴当CD⊥AB时,CD=$\frac{1}{2}$AC=2,
此时,EF=2CD=2×2=4,
∴EF的最小值是4.
故选(C)
点评 本题主要考查了轴对称的性质、直角三角形的性质的综合应用,解决问题的关键是运用垂线段最短以及直角三角形斜边上的中线性质进行判断.

练习册系列答案
相关题目
5.电脑病毒传播快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.若每轮感染中平均一台电脑会感染x台电脑,则下面所列方程中正确的是( )
| A. | x(x+1)=81 | B. | 1+x+x2=81 | C. | (1+x)2=81 | D. | 1+(1+x)2=81 |
7.16的算术平方根是( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 2 |
 ,电子表上实际显示的时间为16:25:08.
,电子表上实际显示的时间为16:25:08. 如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)
如图所示的圆柱体中底面圆的半径是$\frac{2}{π}$,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是$\sqrt{13}$.(结果保留根号)