题目内容
 如图,已知四边形ABCD为正方形,E,F为AB、CD的中点,AD=2,△AGF是由△ADF折叠而来的,连接GI,使得GI⊥AB.
如图,已知四边形ABCD为正方形,E,F为AB、CD的中点,AD=2,△AGF是由△ADF折叠而来的,连接GI,使得GI⊥AB.(1)求GI的长;
(2)求△AIG的面积.
考点:正方形的性质,翻折变换(折叠问题)
专题:
分析:(1)根据翻折的性质可得∠DAF=∠GAF,根据两直线平行,内错角相等可得∠DAF=∠AFH,然后求出∠GAF=∠AFH,再根据等角对等边可得AH=HF,设AH=x,表示出EH,再利用勾股定理列出方程求出x,然后根据△AEH和△AIG相似,利用相似三角形对应边成比例列式计算即可得解;
(2)利用相似三角形对应边成比例列式求出AI,再根据三角形的面积公式列式计算即可得解.
(2)利用相似三角形对应边成比例列式求出AI,再根据三角形的面积公式列式计算即可得解.
解答:解:(1)∵△AGF是由△ADF折叠而来,
∴∠DAF=∠GAF,AG=AD,
∵E,F为AB、CD的中点,
∴EF=AD,AE=
×2=1,
∴∠DAF=∠AFH,
∴∠GAF=∠AFH,
∴AH=FH,
设AH=x,则EH=2-x,
在Rt△AEH中,AE2+EH2=AH2,
即12+(2-x)2=x2,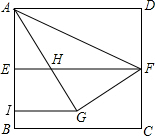
解得x=
,
EH=2-
=
,
∵EF⊥AB,GI⊥AB,
∴EF∥GI,
∴△AEH∽△AIG,
∴
=
,
即
=
,
解得GI=
;
(2)∵△AEH∽△AIG,
∴
=
,
即
=
,
解得AI=
,
△AIG的面积=
×
×
=
.
∴∠DAF=∠GAF,AG=AD,
∵E,F为AB、CD的中点,
∴EF=AD,AE=
| 1 |
| 2 |
∴∠DAF=∠AFH,
∴∠GAF=∠AFH,
∴AH=FH,
设AH=x,则EH=2-x,
在Rt△AEH中,AE2+EH2=AH2,
即12+(2-x)2=x2,

解得x=
| 5 |
| 4 |
EH=2-
| 5 |
| 4 |
| 3 |
| 4 |
∵EF⊥AB,GI⊥AB,
∴EF∥GI,
∴△AEH∽△AIG,
∴
| AH |
| AG |
| EH |
| GI |
即
| ||
| 2 |
| ||
| GI |
解得GI=
| 6 |
| 5 |
(2)∵△AEH∽△AIG,
∴
| AE |
| AI |
| AH |
| AG |
即
| 1 |
| AI |
| ||
| 2 |
解得AI=
| 8 |
| 5 |
△AIG的面积=
| 1 |
| 2 |
| 6 |
| 5 |
| 8 |
| 5 |
| 24 |
| 25 |
点评:本题考查了正方形的性质,翻折变换的性质,相似三角形的判定与性质,勾股定理,熟记翻折的性质并利用勾股定理列方程求出AH、EH的长是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
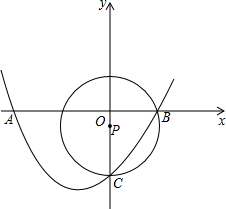 已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b=
已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b= 如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.