题目内容
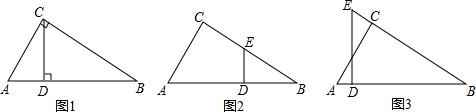
12.(1)如图1,CD是Rt△ABC斜边AB上的高,图中有与∠A相等的角吗?为什么?(2)如图2,把图1中的CD平移到ED,图中还有与∠A相等的角吗?为什么?
(3)如图3,把图1中的CD平移到ED,交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
分析 (1)由∠ACB=90°,得到∠A+∠B=90°根据CD是斜边AB上的高,得到∠ADC=∠BDC=90°,等量代换得到结论;
(2)根据平移的性质得到DE⊥AB,于是得到∠DEB+∠B=90°,在Rt△ABC中,∠A+∠B=90°,等量代换得到结论;
(3)方法与(2)相同.
解答 解:(1)图中有与∠A相等的角,
理由:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD是斜边AB上的高,
∴∠ADC=∠BDC=90°,
∴∠DCB+∠B=90°,
∴∠A=∠DCB;
(2)∠A=∠DEB;
理由:∵CD平移到ED,
∴DE⊥AB,
∴∠DEB+∠B=90°,
在Rt△ABC中,∠A+∠B=90°,
∴∠DEB+∠B=90°,
∴∠A=∠DEB;
(3)∠A=∠DEB;
理由:∵CD平移到ED,
∴DE⊥AB,
∴∠DEB+∠B=90°,
在Rt△ABC中,∠A+∠B=90°,
∴∠DEB+∠B=90°,
∴∠A=∠DEB.
点评 本题考查了平移的性质,直角三角形的性质,熟练掌握平移的性质是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.已知a=$\frac{\sqrt{5}+2}{\sqrt{5}-2}$,b=$\frac{\sqrt{5}-2}{\sqrt{5}+2}$,求$\sqrt{\frac{a+b}{ab}}$的值.
2.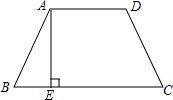 如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
 如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )
如图所示,在梯形ABCD中,∠ABC=60°,AB=CD=AD,过点A作AE⊥BC于点E,AE=3,CE=3$\sqrt{3}$,则梯形ABCD的周长与面积分别是( )| A. | 8,9$\sqrt{3}$ | B. | 10$\sqrt{3}$,9$\sqrt{3}$ | C. | 9$\sqrt{3}$,10$\sqrt{3}$ | D. | 8$\sqrt{3}$,9$\sqrt{3}$ |
 如图,依图填空:
如图,依图填空: