题目内容
17.若$\frac{1}{3}$x2my2与-2xyn是同类项,则mn=1.分析 根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程2m=1,n=2,求出m,n的值,再代入代数式计算即可.
解答 解:∵$\frac{1}{3}$x2my2与-2xyn是同类项,
∴2m=1,n=2,
∴m=$\frac{1}{2}$,n=2,
∴mn=1.
故答案为:1.
点评 本题考查的是同类项的定义,即所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.若a,b互为相反数(a≠0),则关于x的方程ax+b=0的解是( )
| A. | x=1 | B. | x=-1 | C. | x=1或x=-1 | D. | 不能确定 |
9.一只不透明的袋子中装有4个质地,大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算两个小球数字之和.记录后将小球放回袋中搅匀.进行重复实验,实验数据如表:
解答下列问题:
(1)如果实验继续进行下去,根据上表提供数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是.
(2)如果摸出这两个小球上数字之和为9的概率是$\frac{1}{3}$,那么x的值可以取7吗?请用列表或画树状图的方法说明理由.
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8“出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8“出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表提供数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是.
(2)如果摸出这两个小球上数字之和为9的概率是$\frac{1}{3}$,那么x的值可以取7吗?请用列表或画树状图的方法说明理由.
7.若x2+y2=10,xy=3,则x+y的值为( )
| A. | 12 | B. | 4 | C. | -4 | D. | ±4 |
 如图,∠1=45°,∠2=135°,l1与l2平行吗?试说明理由.
如图,∠1=45°,∠2=135°,l1与l2平行吗?试说明理由.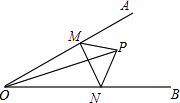 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,求MN的长.
如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,求MN的长. 如图,AE∥CD,∠1=37°,∠D=54°,求∠2和∠BAE的度数.
如图,AE∥CD,∠1=37°,∠D=54°,求∠2和∠BAE的度数.