题目内容
8.已知关于x的一元二次方程x2+(2m+1)x+(m-2)2=0有一个根为0,求这个方程根的判别式的值.分析 首先根据x的一元二次方程x2+(2m+1)x+(m-2)2=0有一个根为0,可得(m-2)2=0,据此求出m的值是多少;然后根据△=b2-4ac,求出这个方程根的判别式的值是多少即可.
解答 解:∵关于x的一元二次方程x2+(2m+1)x+(m-2)2=0有一个根为0,
∴(m-2)2=0,
解得m=2,
∴原方程是x2+5x=0,
∴△=b2-4ac
=52-4×1×0
=25
∴这个方程根的判别式的值是25.
点评 此题主要考查了整式的加减-化简求值,要熟练掌握,解答此题的关键是要明确:给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.

练习册系列答案
相关题目
3.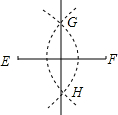 任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
 任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )
任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是( )| A. | △EGH为等腰三角形 | B. | △EGF为等边三角形 | ||
| C. | 四边形EGFH为菱形 | D. | △EHF为等腰三角形 |
13.如图所示,用量角器度量∠AOB,可以读出∠AOB的度数为( )


| A. | 45° | B. | 55° | C. | 125° | D. | 135° |
17.当0<x<1时,x2、x、$\frac{1}{x}$的大小顺序是( )
| A. | x2$<x<\frac{1}{x}$ | B. | $\frac{1}{x}$<x<x2 | C. | $\frac{1}{x}<{x}^{2}$<x | D. | x<x2<$\frac{1}{x}$ |
 已知线段AB,利用无刻度的直尺和圆规,作线段AC,使点B为线段AC的中点,要求:不写作法,保留作图痕迹.
已知线段AB,利用无刻度的直尺和圆规,作线段AC,使点B为线段AC的中点,要求:不写作法,保留作图痕迹.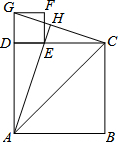 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.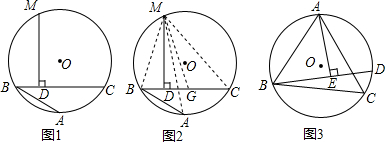
 如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于60度.
如图所示,一艘船从A点出发,沿东北方向航行至B,再从B点出发沿南偏东15°方向航行至C点,则∠ABC等于60度. 请用割补法作图,将一个锐角三角形经过一次或两次分割后,重新拼成一个与原三角形面积相等的平行四边形(只要求用一种方法画出图形,把相等的线段作相同的标记).
请用割补法作图,将一个锐角三角形经过一次或两次分割后,重新拼成一个与原三角形面积相等的平行四边形(只要求用一种方法画出图形,把相等的线段作相同的标记).