题目内容
1. 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34)
分析 作AD⊥BC,垂足为D.根据坡度相同,判断出∠BAD=∠CAD=70°×$\frac{1}{2}$=35°,然后证出△BAD≌△CAD,进而求出AB的长,乘以2即可而得到一楼到二楼的楼梯总长度.
解答 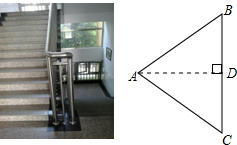 解:作AD⊥BC,垂足为D.
解:作AD⊥BC,垂足为D.
∵CA、AB的而坡度相同,
∴∠BAD=∠CAD=70°×$\frac{1}{2}$=35°,
在△BAD和△CAD中,
$\left\{\begin{array}{l}∠BAD=∠CAD\\ AD=AD\\∠BDA=∠CDA\end{array}\right.$,
∴△BAD≌△CAD(ASA).
∴BD=CD=5×$\frac{1}{2}$=2.5,
在Rt△ABD中,$\frac{BD}{AB}$=sin35°,
∴AB=$\frac{BD}{sin35°}$=$\frac{2.5}{0.57}$≈4.4米.
楼梯的总长度为4.4×2=8.8米.
点评 本题考查了解直角三角形的应用---坡度坡角问题,熟悉等腰三角形的性质和解直角三角形是解题的关键.

练习册系列答案
相关题目
16.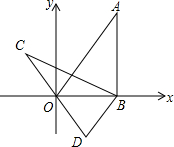 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (-4,2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,2) | D. | (-2$\sqrt{3}$,4) |
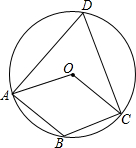 如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°.
如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=60°. 如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.
如图,以?ABCD的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD.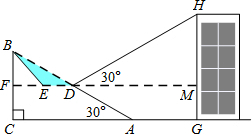 如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).
如图,已知斜坡AB长60m,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.732).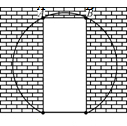 温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.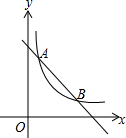 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.