题目内容
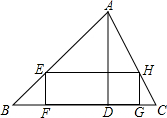 如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.
如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.(1)写出y与x的函数关系式.
(2)x取多少时,EFGH是正方形.
考点:相似三角形的应用
专题:
分析:(1)首先得出△AEH∽△ABC,进而利用相似三角形的性质求出即可;
(2)利用正方形的判定方法得出邻边关系进而得出答案.
(2)利用正方形的判定方法得出邻边关系进而得出答案.
解答: 解:(1)如图所示:
解:(1)如图所示:
∵EH∥BC,
∴△AEH∽△ABC,
∴
=
,
∵BC边为4厘米,BC边上的高AD为3厘米,设EF=x厘米,FG=y厘米,
∴
=
,
则y=-
x+4;
(2)当四边形EFGH是正方形,
故EF=EH,
则x=-
x+4,
解得:x=
.
答:x取
时,四边形EFGH是正方形.
 解:(1)如图所示:
解:(1)如图所示:∵EH∥BC,
∴△AEH∽△ABC,
∴
| AN |
| AD |
| EH |
| BC |
∵BC边为4厘米,BC边上的高AD为3厘米,设EF=x厘米,FG=y厘米,
∴
| 3-x |
| 3 |
| y |
| 4 |
则y=-
| 4 |
| 3 |
(2)当四边形EFGH是正方形,
故EF=EH,
则x=-
| 4 |
| 3 |
解得:x=
| 12 |
| 7 |
答:x取
| 12 |
| 7 |
点评:此题主要考查了相似三角形的判定与性质以及正方形的判定,得出△AEH∽△ABC是解题关键.

练习册系列答案
相关题目
 如图,已知平面直角坐标系中,A,B坐标为A(-1,3),B(-4,2)
如图,已知平面直角坐标系中,A,B坐标为A(-1,3),B(-4,2)
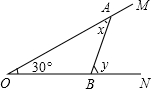 如图,∠MON=30°,点A、B分别是OM、ON两边上的一个动点;若∠OAB=x(度),∠ABN=y(度).
如图,∠MON=30°,点A、B分别是OM、ON两边上的一个动点;若∠OAB=x(度),∠ABN=y(度).