题目内容
 如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.
如图,在△ABC中,∠C=90°,AC=BC,BD平分∠ABC,DE⊥AB于点E,若△BCD与△ABC的面积之比是3:8,求△ADE与△ABC的面积之比.考点:角平分线的性质,等腰直角三角形
专题:
分析:求出CD=DE,根据三角形面积公式求出DE:BC,根据相似得出△ADE与△ABC的面积之比等于相似比(DE:BC)的平方,代入求出即可.
解答:解:∵∠C=90°,BD平分∠ABC,DE⊥AB,
∴CD=DE,
∵AC=BC,∵
由勾股定理得:AB=
=
AC=
BC,
∵△BCD与△ABC的面积之比是3:8,
∴(
×BC×CD):(
×BC×AC)=3:8,
∴
=
,
∵CD=DE,BC=AC,
∴
=
,
∵DE⊥AB,
∴∠DEA=∠C=90°,
∵∠A=∠A,
∴△AED∽△ACB,
∴
=(
)2=(
)2=
,
即△ADE与△ABC的面积之比是9:64.
∴CD=DE,
∵AC=BC,∵
由勾股定理得:AB=
| AC2+AC2 |
| 2 |
| 2 |
∵△BCD与△ABC的面积之比是3:8,
∴(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CD |
| AC |
| 3 |
| 8 |
∵CD=DE,BC=AC,
∴
| DE |
| BC |
| 3 |
| 8 |
∵DE⊥AB,
∴∠DEA=∠C=90°,
∵∠A=∠A,
∴△AED∽△ACB,
∴
| S△ADE |
| S△ABC |
| DE |
| BC |
| 3 |
| 8 |
| 9 |
| 64 |
即△ADE与△ABC的面积之比是9:64.
点评:本题考查了角平分线性质,相似三角形的性质和判定的应用,主要考查学生的推理和计算能力.

练习册系列答案
相关题目
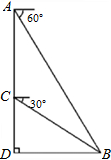 小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)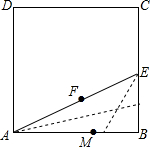 如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.
如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.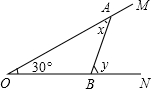 如图,∠MON=30°,点A、B分别是OM、ON两边上的一个动点;若∠OAB=x(度),∠ABN=y(度).
如图,∠MON=30°,点A、B分别是OM、ON两边上的一个动点;若∠OAB=x(度),∠ABN=y(度).