题目内容
 如图,AB是⊙O的直径,AC、BC是弦,D是
如图,AB是⊙O的直径,AC、BC是弦,D是 |
| BC |
(1)求证:BC=2DE;
(2)求tan∠CBD的值.
考点:垂径定理,勾股定理,三角形中位线定理,圆周角定理,锐角三角函数的定义
专题:几何综合题
分析:(1)连接OD交BC于点H,由全等三角形的判定定理得出△OBH≌△ODE,故∠OHB=∠C=90°,OH是△ABC的中位线,由中位线的性质即可得出结论;
(2)由(1)可知OH为△ABC的中位线,故OH=
AC=3,OD=OB=5,DH=OD-OH=2,由勾股定理求出DE的长,根据锐角三角函数的定义即可求出结论.
(2)由(1)可知OH为△ABC的中位线,故OH=
| 1 |
| 2 |
解答: 解:(1)方法一:连接OD交BC于点H,
解:(1)方法一:连接OD交BC于点H,
∵D是
的中点,
∴∠CBD=∠ABC,
在△OBH与△ODE中,
,
∴△OBH≌△ODE,
∴∠OHB=∠C=90°,
∴OH是△ABC的中位线,
∴DE=BH=
BC,
∴BC=2DE;
方法二:先设DE交⊙O于点G,
=
=
,BC=DG=2DE.
(2)方法一:∵由(1)可知OH为△ABC的中位线,
∴OH=
AC=3,OD=OB=5,DH=OD-OH=2,
∴BH=
=4,
∴DE=4,
∴tan∠CBD=
=
=
.
方法二:连接AD,DE2=AE•BE,设AE=x>5,DE2=x•(10-x),
∵DE=
BC=4,
∴42=x•(10-x),解得x=8或x=2(舍去),
∴tan∠CBD=tan∠DAE=
=
=
.
 解:(1)方法一:连接OD交BC于点H,
解:(1)方法一:连接OD交BC于点H,∵D是
 |
| BC |
∴∠CBD=∠ABC,
在△OBH与△ODE中,
|
∴△OBH≌△ODE,
∴∠OHB=∠C=90°,
∴OH是△ABC的中位线,
∴DE=BH=
| 1 |
| 2 |
∴BC=2DE;
方法二:先设DE交⊙O于点G,
 |
| CD |
 |
| DB |
 |
| BG |
(2)方法一:∵由(1)可知OH为△ABC的中位线,
∴OH=
| 1 |
| 2 |
∴BH=
| 52-32 |
∴DE=4,
∴tan∠CBD=
| DH |
| BH |
| 2 |
| 4 |
| 1 |
| 2 |
方法二:连接AD,DE2=AE•BE,设AE=x>5,DE2=x•(10-x),
∵DE=
| 1 |
| 2 |
∴42=x•(10-x),解得x=8或x=2(舍去),
∴tan∠CBD=tan∠DAE=
| DE |
| AE |
| 4 |
| 8 |
| 1 |
| 2 |
点评:本题考查的是垂径定理、勾股定理、三角形中位线的定理及锐角三角函数的定义,根据题意作出辅助线.构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
函数y=
的自变量x的取值范围是( )
| -1-2x |
A、x≥-
| ||
B、x≤-
| ||
C、x≥
| ||
D、x≤
|
 如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C.在图中画出△A′B′C,并分别写出点A′、B′、C的坐标.
如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C.在图中画出△A′B′C,并分别写出点A′、B′、C的坐标.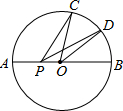 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点, 表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是
表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是