题目内容
已知在△ABC中,∠BAC=90°,AD⊥BC于D,AB=2
,DC=4,则AD的长为 .
| 3 |
考点:相似三角形的判定与性质,勾股定理
专题:计算题
分析:根据题意画出相应的图形,如图所示,由AD与BC垂直,得到三角形ABD与三角形ACD都为直角三角形,可得出一对直角相等,在直角三角形ABD中,根据直角三角形的两锐角互余得到一对角互余,再由直角三角形ABC的两锐角互余得到另一对角互余,根据同角的余角相等可得出一对角相等,根据两对对应角相等的两三角形相似可得出三角形ABD与三角形ACD相似,由相似得比例列出比例式,设AD为x,在直角三角形ABD中,由AB及AD,利用勾股定理表示出BD,将DC,BD及AD代入比例式中,列出关于x的方程,求出方程的解得出x的值,即为AD的长.
解答:解:根据题意画出相应的图形,如图所示:

∵AD⊥BC,∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
又∠BAC=90°,∴∠B+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△CAD,
∴AD2=BD•DC,
设AD=x,在Rt△ABD中,AD=x,AB=2
,
根据勾股定理得:BD=
=
,
又BD=4,
∴x2=4
,
两边平方得:x4=16(12-x2),即x4+16x2-192=0,
因式分解得:(x2+24)(x2-8)=0,
可得:x2=-24(舍去),x2=8,
解得:x=2
,或x=-2
(舍去),
则CD=2
.
故答案为:2

∵AD⊥BC,∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
又∠BAC=90°,∴∠B+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△CAD,
∴AD2=BD•DC,
设AD=x,在Rt△ABD中,AD=x,AB=2
| 3 |
根据勾股定理得:BD=
| AB2-AD2 |
| 12-x2 |
又BD=4,
∴x2=4
| 12-x2 |
两边平方得:x4=16(12-x2),即x4+16x2-192=0,
因式分解得:(x2+24)(x2-8)=0,
可得:x2=-24(舍去),x2=8,
解得:x=2
| 2 |
| 2 |
则CD=2
| 2 |
故答案为:2
| 2 |
点评:此题考查了相似三角形的判定与性质,勾股定理,以及垂直的定义,利用了转化的思想,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
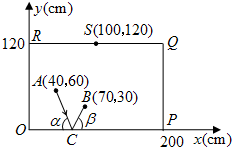 实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.
实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.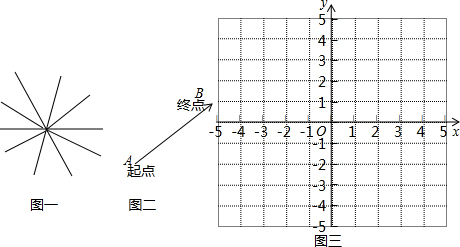
 如图所示,堆放的一堆钢管共110根,最上面的一层有5根,每往下一层就增加一根,如果每根钢管的直径为10厘米,那么这堆钢管的总高度是
如图所示,堆放的一堆钢管共110根,最上面的一层有5根,每往下一层就增加一根,如果每根钢管的直径为10厘米,那么这堆钢管的总高度是 如图,AB是⊙O的直径,AC、BC是弦,D是
如图,AB是⊙O的直径,AC、BC是弦,D是
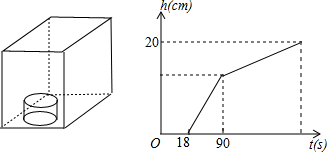 .水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.
.水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.