题目内容
13．计算：（-2）0-2-1=$\frac{1}{2}$．分析 原式利用零指数幂、负整数指数幂法则计算即可得到结果．
解答 解：原式=1-$\frac{1}{2}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，点A在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，点B在y轴上，且AO=AB，若△ABO的面积为12，则k的值为-12．
4．甲、乙、丙、丁四名射手在预选赛中所得的平均环数$\overline{x}$及其方差s2如表所示，则选拔 一名参赛的人选，应是（ ）
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 7 | 8 | 8 | 7 |
| s2 | 6.3 | 6.3 | 7 | 8.7 |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
1．若点P（x，y）位于第二象限，且y≤x+4，x、y为整数，符合上述条件的点P共有（ ）个．
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
8．
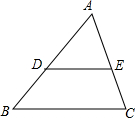如图，点D、E分别在△ABC的边AB、AC上，下列条件不能使△ADE∽△ABC相似的是（ ）
如图，点D、E分别在△ABC的边AB、AC上，下列条件不能使△ADE∽△ABC相似的是（ ）| A． | DE∥BC | B． | AD：AB=DE：BC | C． | AD：DB=AE：EC | D． | ∠BDE+∠DBC=180° |
18．若分式$\frac{{a}^{2}}{a-2}$有意义，则a的取值范围是（ ）
| A． | a≠2 | B． | a≠0 | C． | a≠2且a≠0 | D． | 一切实数 |
如图，四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP垂直x轴于点P，连结AC交NP于Q，连结MQ．
2．下列命题中，有几个真命题（ ）
①同位角相等
②直角三角形的两个锐角互余
③平行四边形的对角线互相平分且相等
④对顶角相等．
①同位角相等
②直角三角形的两个锐角互余
③平行四边形的对角线互相平分且相等
④对顶角相等．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，AB∥EM∥DC，AE=ED，EF∥BC，EF=12cm，则BC的长为24cm．