题目内容
17．如图①，正方形ABDE、CDFI、EFGH的面积分别为17、10、13，图②中的DPQR为矩形，对照图②求图①中ABCIGH的面积．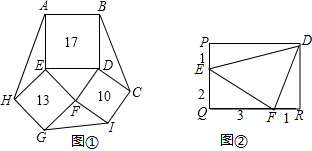
分析 首先求出△BCD，△GFI，△AEH的面积即可，然后△DEF的面积通过图乙求解．
解答 解：∵DF=DC，DE=DB，且∠EDF+∠BDC=180°，
根据三角形的面积公式得S△AHE=S△DEF，
同理S△BDC=S△GFI=S△DEF，
S△AHE+S△BDC+S△GFI=3×S△DEF，
S△DEF=3×4-2-3-1.5=5.5，
∴六边形ABCIGH的面积为S△AHE+S△BDC+S△GFI+S△DEF+17+13+10
=62．
答：六边形ABCIGH的面积为62．
点评 此题考查了正方形的性质以及三角形面积的计算．注意解本题的关键是找到：S△AHE+S△BDC+S△GFI=3×S△DEF．
练习册系列答案
阅读快车系列答案
相关题目
如图所示：△AOB的三个顶点的坐标分别为O（0，0），A（5，0），B（1，4）．
2．已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值，如表：
（1）求二次函数解析式？
（2）当x为何值，y有最小值，最小值是多少？
（3）若m＜0，点A（m，y1）B（m+1，y2）都在该函数图象上，试比较y1、y2的大小．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
（2）当x为何值，y有最小值，最小值是多少？
（3）若m＜0，点A（m，y1）B（m+1，y2）都在该函数图象上，试比较y1、y2的大小．