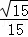题目内容
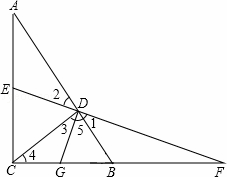
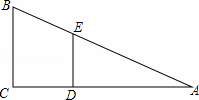
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
(1)求证:FD2=FB•FC;
(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.
考点: 相似三角形的判定与性质;直角三角形斜边上的中线.
专题: 综合题.
分析: (1)要求证:FD2=FB•FC,只要证明△FBD∽△FDC,从而转化为证明∠FDC=∠FBD;
(2)要证DG⊥EF,只要证明∠5+∠1=90°,转化为证明∠3=∠4即可.
解答: (1)证明:∵E是Rt△ACD斜边中点,
∴DE=EA,
∴∠A=∠2,(1分)
∵∠1=∠2,
∴∠1=∠A,(2分)
∵∠FDC=∠CDB+∠1=90°+∠1,∠FBD=∠ACB+∠A=90°+∠A,
∴∠FDC=∠FBD,
∵∠F是公共角,
∴△FBD∽△FDC.(4分)
∴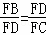 .
.
∴FD2=FB•FC.(6分)
(2)GD⊥EF.(7分)
理由如下:
∵DG是Rt△CDB斜边上的中线,
∴DG=GC.
∴∠3=∠4.
由(1)得∵△FBD∽△FDC,
∴∠4=∠1,
∴∠3=∠1.(9分)
∵∠3+∠5=90°,
∴∠5+∠1=90°.
∴DG⊥EF.(10分)
点评: 证明线段的积相等可以转化为证明三角形相似,证明两直线垂直转化为证明形成的角是直角.

练习册系列答案
相关题目
 的图象上,则该函数的图象位于第 象限.
的图象上,则该函数的图象位于第 象限.
 ,α是锐角,求tan(9O°﹣α),sinα,cosα的值.
,α是锐角,求tan(9O°﹣α),sinα,cosα的值. ,则该正六边形的边长是( )
,则该正六边形的边长是( )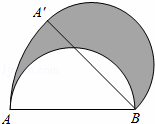
 D. 4π
D. 4π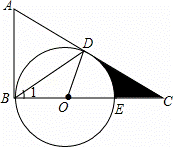
 ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )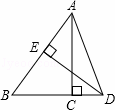
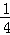 B.
B. 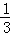 C.
C.  D.
D.