题目内容
18. 如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )
如图,已知⊙O的内接四边形ABCD,AD=$\sqrt{2}$,CD=1,半径为1,则∠B的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
分析 连接OA,OD,OC,根据勾股定理的逆定理得到∠AOD=90°,根据等边三角形的性质得到∠COD=60°,根据圆周角定理即可得到结论.
解答  解:连接OA,OD,OC,
解:连接OA,OD,OC,
∵AD=$\sqrt{2}$,OA=OD=1,
∴OA2+OD2=2=AD2,
∴∠AOD=90°,
∵OD=OC=CD=1.
∴△COD是等边三角形,
∴∠COD=60°,
∴∠AOC=150°,
∴∠B=$\frac{1}{2}∠$AOC=75°,
故选C.
点评 本题考查了圆内接四边形的性质,圆周角定理,勾股定理的逆定理,正确的作出辅助线是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
6.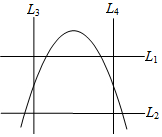 小明将如图两水平线l1、l2的其中一条当成x轴,且向右为正方向;两条直线l3、l4的其中一条当成y轴,且向上为正方向,并在此坐标平面中画出二次函数y=ax2-2a2x+1的图象,则( )
小明将如图两水平线l1、l2的其中一条当成x轴,且向右为正方向;两条直线l3、l4的其中一条当成y轴,且向上为正方向,并在此坐标平面中画出二次函数y=ax2-2a2x+1的图象,则( )
 小明将如图两水平线l1、l2的其中一条当成x轴,且向右为正方向;两条直线l3、l4的其中一条当成y轴,且向上为正方向,并在此坐标平面中画出二次函数y=ax2-2a2x+1的图象,则( )
小明将如图两水平线l1、l2的其中一条当成x轴,且向右为正方向;两条直线l3、l4的其中一条当成y轴,且向上为正方向,并在此坐标平面中画出二次函数y=ax2-2a2x+1的图象,则( )| A. | l1为x轴,l3为y轴 | B. | l2为x轴,l3为y轴 | C. | l1为x轴,l4为y轴 | D. | l2为x轴,l4为y轴 |
7.若一批校服按七折出售,每件为x元,则这批校服每件的原价为( )
| A. | x•70% | B. | $\frac{x}{70%}$ | C. | x•30% | D. | $\frac{x}{30%}$ |
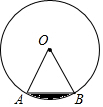 如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.
如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.
 如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D.已知∠APB=60°,AC=2,那么AD的长为$\frac{2\sqrt{21}}{7}$.
如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D.已知∠APB=60°,AC=2,那么AD的长为$\frac{2\sqrt{21}}{7}$.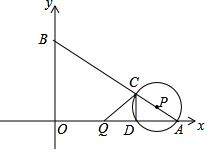 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.