题目内容
6．
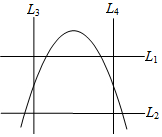小明将如图两水平线l1、l2的其中一条当成x轴，且向右为正方向；两条直线l3、l4的其中一条当成y轴，且向上为正方向，并在此坐标平面中画出二次函数y=ax2-2a2x+1的图象，则（ ）| A． | l1为x轴，l3为y轴 | B． | l2为x轴，l3为y轴 | C． | l1为x轴，l4为y轴 | D． | l2为x轴，l4为y轴 |
分析 根据抛物线的开口向下，可得a＜0，求出对称轴为：直线x=2a，则可确定l4为y轴，再根据图象与y轴交点，可得出l2为x轴，即可得出答案．
解答 解：∵抛物线的开口向下，
∴a＜0，
∴抛物线与y轴的负半轴相交，
∴l2为x轴，l4为y轴．
故选：D．
点评 本题考查了二次函数的性质，开口方向由a确定，与y轴的交点由c确定，左同右异确定b的符号．
练习册系列答案
相关题目
16．某工程要在x天内完成，现由甲先做3天，乙再参加合做，正好如期完成．若甲独做需12天完成，乙独做需8天完成，则下列方程正确的是（ ）
| A． | $\frac{x}{12}$+$\frac{x-3}{8}$=1 | B． | $\frac{x+3}{12}$+$\frac{x-3}{8}$=1 | C． | $\frac{x}{12}$+$\frac{x}{8}$=1 | D． | $\frac{x+3}{12}$+$\frac{x}{8}$=1 |
17．下列命题是假命题的是（ ）
| A． | 全等三角形对应角相等 | |
| B． | 如果实数x满足x2＞0，那么x≠0 | |
| C． | 如果两个角相等，那么它们是对顶角 | |
| D． | 对顶角相等 |
如图，抛物线y=$-\frac{1}{2}$x2+bx+c与x轴交于A，B两点，与y轴交于点C，已知A（-1，0），B（4，0），点D（m，n）是线段BC上的一个动点（点D不与B，C重合），过点D作x轴的垂线与抛物线相交于点F，垂足为E．
如图，三角形△ABC中，∠OAB=∠AOB=15°，点B在x轴的正半轴，坐标为B（6$\sqrt{3}$，0）．OC平分∠AOB，点M在OC的延长线上，点N为边OA上的点，则MA+MN的最小值是3$\sqrt{3}$．
18．
如图，已知⊙O的内接四边形ABCD，AD=$\sqrt{2}$，CD=1，半径为1，则∠B的度数为（ ）
如图，已知⊙O的内接四边形ABCD，AD=$\sqrt{2}$，CD=1，半径为1，则∠B的度数为（ ）| A． | 60° | B． | 70° | C． | 75° | D． | 80° |
4．标号为A、B、C、D的四个盒子中所装有的白球和黑球数如下，则下列盒子最易摸到黑球的是（ ）
| A． | 12个黑球和4个白球 | B． | 10个黑球和10个白球 | ||
| C． | 4个黑球和2个白球 | D． | 10个黑球和5个白球 |