题目内容
11.已知m是$\sqrt{5}$的小数部分,则$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}-2}$的值( )| A. | $\frac{4}{5}\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | -4 | D. | 4 |
分析 由题意可知:m=$\sqrt{5}$-2:
(1)先利用完全平方公式因式分解,再进一步代入求得答案即可;
(2)先化简二次根式,再进一步代入求得答案即可.
解答 解:∵2$<\sqrt{5}$<3,
∴m=$\sqrt{5}$-2,
∵$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}-2}$=|m-$\frac{1}{m}$|=|$\sqrt{5}$-2-$\sqrt{5}$-2|=4,
故选D.
点评 此题考查二次根式的化简求值,掌握完全平方公式和无理数的估算是解决问题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
1.我市2016年某一周每天的最高气温(单位:℃)统计如下:10,16,12,11,14,12,13,则这组数据的众数是( )
| A. | 11 | B. | 12 | C. | 14 | D. | 16 |
 如图,在△ABC中,DE∥BC,EF∥AB,∠A=60°,∠C=70°,则∠DEF=50°.
如图,在△ABC中,DE∥BC,EF∥AB,∠A=60°,∠C=70°,则∠DEF=50°.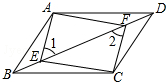 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.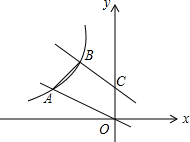 直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.
直线y=-x+1交y轴于C点,直线y=-$\frac{1}{2}$x,两条直线分别交双曲线y=$\frac{k}{x}$(x<0)于B、A两点,若$\frac{OA}{BC}$=$\frac{\sqrt{10}}{2}$.