��Ŀ����
5�������и�ʽ������Ӧ�Ĵ������x-7��$\frac{1}{3}$x��4ab��$\frac{2}{3a}$��5-$\frac{3}{x}$��y��$\frac{s}{t}$��x+$\frac{1}{3}$��$\frac{x}{7}$$+\frac{y}{7}$��x2$+\frac{x}{2}$+1��$\frac{m-1}{m+1}$��8a3x��-1
����ʽ����{ ��}��
����ʽ����{ ��}��
��ʽ����{ ��}��
���� ���ݵ���ʽ������ʽ����ʽ�Ķ����ɣ�
��� �⣺����ʽ�У�$\frac{1}{3}$x��4ab��y��8a3x��-1��
����ʽ�У�x-7��x+$\frac{1}{3}$��$\frac{x}{7}$$+\frac{y}{7}$��x2$+\frac{x}{2}$+1��
��ʽ�У�$\frac{1}{3}$x��4ab��y��8a3x��-1��x-7��x+$\frac{1}{3}$��$\frac{x}{7}$$+\frac{y}{7}$��x2$+\frac{x}{2}$+1��
�ʴ�Ϊ��$\frac{1}{3}$x��4ab��y��8a3x��-1��x-7��x+$\frac{1}{3}$��$\frac{x}{7}$$+\frac{y}{7}$��x2$+\frac{x}{2}$+1��$\frac{1}{3}$x��4ab��y��8a3x��-1��x-7��x+$\frac{1}{3}$��$\frac{x}{7}$$+\frac{y}{7}$��x2$+\frac{x}{2}$+1��
���� ������Ҫ���������ʽ�����յ���ʽ������ʽ����ʽ�Ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
�����Ŀ
14��$3����-\frac{4}{7}���£�-\frac{3}{7}��-��-1��^{2}$��ֵΪ��������
| A�� | 3 | B�� | -3 | C�� | 5 | D�� | -5 |
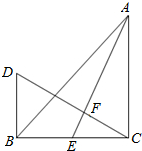 ��ͼ����ABC�У���ACB=90�㣬AC=BC��AE��BC�ϵ����ߣ���C��CF��AE������ΪF�㣬��B��BD��BC��CF���ӳ�����D�㣮��BD=3cm�����߶�AC�ij���
��ͼ����ABC�У���ACB=90�㣬AC=BC��AE��BC�ϵ����ߣ���C��CF��AE������ΪF�㣬��B��BD��BC��CF���ӳ�����D�㣮��BD=3cm�����߶�AC�ij���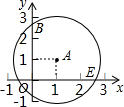 ��ͼ����ƽ��ֱ������ϵ�У���A��1��1��ΪԲ�ģ�2Ϊ�뾶����A�����A���������ύ������꣮
��ͼ����ƽ��ֱ������ϵ�У���A��1��1��ΪԲ�ģ�2Ϊ�뾶����A�����A���������ύ������꣮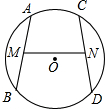 ��ͼ��AB��CD�ǡ�O�������ң�M��N�ֱ�ΪAB��CD���е㣬�ҡ�AMN=��CNM��AB=6����CD=6��
��ͼ��AB��CD�ǡ�O�������ң�M��N�ֱ�ΪAB��CD���е㣬�ҡ�AMN=��CNM��AB=6����CD=6�� ��ֻС����ͬʱ�������ԭ������������������������У��������ظ��������У������ϵ��ٶ���ÿ����1.5����λ���ȣ������ϵ��ٶ���ÿ����2����λ���ȣ�t���Ӻ���ֻ�������3.5t����λ���ȣ�x���Ӻ�����ϱ������϶���1.5t����λ���ȣ�
��ֻС����ͬʱ�������ԭ������������������������У��������ظ��������У������ϵ��ٶ���ÿ����1.5����λ���ȣ������ϵ��ٶ���ÿ����2����λ���ȣ�t���Ӻ���ֻ�������3.5t����λ���ȣ�x���Ӻ�����ϱ������϶���1.5t����λ���ȣ�