Question

20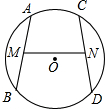．如图，AB，CD是⊙O的两条弦，M，N分别为AB，CD的中点，且∠AMN=∠CNM，AB=6，则CD=6．

Answer 1

分析 连接OM，ON，OA，OC，先根据垂径定理得出AM=$\frac{1}{2}$AB，CN=$\frac{1}{2}$CD，再由∠AMN=∠CNM得出∠NMO=∠MNO，即OM=ON，再由OA=OC可知Rt△AOM≌Rt△CON，故AM=CN，由此即可得出结论．

解答 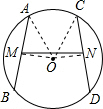证明：连接OM，ON，OA，OC，
∵M、N分别为AB、CD的中点，
∴OM⊥AB，ON⊥CD，
∴AM=$\frac{1}{2}$AB，CN=$\frac{1}{2}$CD，
∵∠AMN=∠CNM，
∴∠NMO=∠MNO，即OM=ON，
在Rt△AOM与Rt△CON中，
$\left\{\begin{array}{l}{OM=ON}\\{OA=OC}\end{array}\right.$，
∴Rt△AOM≌Rt△CON（HL），
∴AM=CN，
∴AB=CD=6．
故答案是：6．

点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．