题目内容
16．
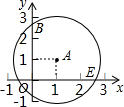如图，在平面直角坐标系中，以A（1，1）为圆心，2为半径作⊙A，求⊙A与两坐标轴交点的坐标．
分析 连接AE，根据勾股定理求出HE的长，根据垂径定理求出⊙A与两坐标轴交点的坐标．
解答 
解：连接AE，
∵AH=1，AE=2，
∴HE=$\sqrt{A{E}^{2}-A{H}^{2}}$=$\sqrt{5}$，
∴⊙A与x轴交点的坐标（-$\sqrt{5}$+1，0）、（$\sqrt{5}$+1，0），
⊙A与y轴交点的坐标（0，-$\sqrt{5}$+1）、（0，$\sqrt{5}$+1）．
点评 本题考查的是垂径定理的应用、坐标与图形的性质和勾股定理的应用，掌握垂直弦的直径平分这条弦是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上．△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1=4，则△A6B6A7的边长为（ ）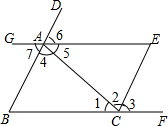
如图，由哪些条件，可得到直线AE∥BF，AB∥CE，直接写出这个条件，不写理由．
如图所示，直线AB、CD被直线EF所截，若∠1=∠2，则AB∥CD；若∠3=∠2，则AB∥CD；若∠2+∠4=180°，则AB∥CD．
已知点A（-1，2），点C（2，1）沿0A方向平移$\sqrt{5}$个单位得出点B，判断四边形0ABC的形状，并证明你的结论；求出直线0A和BC之间的距离．
如图，已知在△ABC中，AD平分∠BAC，BE∥AD，交CA延长线交于点E，F是BE的中点，求证：AF⊥BE．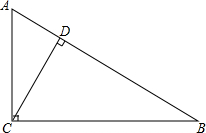
如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，∠A=60°，且AC=2，CD=$\sqrt{3}$，CB=2$\sqrt{3}$，AD=1，BD=3，试找出图中各对相似的三角形，并指出它们的相似比．