题目内容

3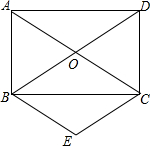．已知，如图，矩形ABCD的对角线AC，BD相交于点O，BE∥AC，CE∥DB．
求证：四边形OBEC是菱形．

分析 先由已知条件证明四边形OBEC是平行四边形，再由矩形的性质得出OB=OC，由菱形的判定方法即可得出结论．

解答 证明：∵BE∥AC，CE∥DB，
∴四边形OBEC是平行四边形，
∵四边形ABCD是矩形，
∴OC=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AC=BD，
∴OB=OC，
∴四边形OBEC是菱形．

点评 本题考查了矩形的性质、平行四边形的判定、菱形的判定；熟练掌握矩形的性质，并能进行推理论证是解决问题的关键．

练习册系列答案
相关题目
13．在三角形的三个外角（一个顶点只取一个外角）中，钝角的个数至少是（　　）
A．3B．2C．1D．0
14．化简或计算：
（1）$\frac{b}{a-b}$+$\frac{a}{a+b}$+$\frac{2ab}{{a}^{2}-{b}^{2}}$      
（2）（$\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$）÷$\frac{x}{x-1}$
（3）$\sqrt{12}$-$\sqrt{18}$-$\sqrt{0.5}$+$\sqrt{\frac{1}{3}}$；          
（4）$\frac{1}{3}$$\sqrt{{x}^{2}y}$×（-$\frac{1}{4}$$\sqrt{\frac{{y}^{2}}{x}}$）÷（-$\frac{1}{6}$$\sqrt{{x}^{2}}y$）
（5）解方程：$\frac{1}{x-3}$+2=$\frac{x-4}{3-x}$．        
（6）解方程：$\frac{1}{y-1}$+$\frac{2}{{y}^{2}+2y-3}$=$\frac{y-1}{{y}^{2}-9}$．
11．先化简，再求值：-$\frac{3}{2}$x-4（$\frac{1}{2}$x-$\frac{1}{6}$y2）+（$\frac{1}{2}$x+$\frac{1}{3}$y2），其中x=-2，y=$\frac{3}{5}$．
18．如图，∠ABE=15°，∠BAD=30°，则∠BED的度数是45度．
8．计算题
（1）（xy2）2-2x（xy4）
（2）（-2x-1）（3x-2）
（3）解不等式2x-4≤3（2-x）并把解集在数轴上表示出来
（4）解不等式组$\left\{\begin{array}{l}{x+3＞0}\\{3（x-1）≤2x-1}\end{array}\right.$并把解集在数轴上表示出来．
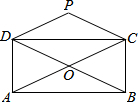15．如图，矩形ABCD的对角线相交于O点，PD∥AC，PC∥BD，PD、PC相交于P点．猜想：四边形PCOD是菱形吗？并说明你的理由．
12．计算：
（1）$\frac{2a}{{a}^{2}-{b}^{2}}$+$\frac{1}{b-a}$                    
（2）1-$\frac{a-3}{a}$÷$\frac{{a}^{2}-2a-3}{{a}^{2}+2a}$．
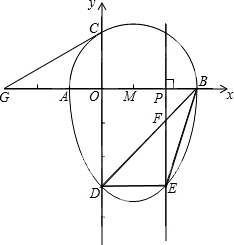13．我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，点A、B、C、D分别是“蛋圆”与坐标轴的交点，AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．“蛋圆”被平行于y轴的直线截得的最大弦长6．
（1）写出“蛋圆”抛物线部分的解析式及自变量的取值范围；
（2）①“蛋圆”被y轴的直线截得的弦CD的长为$\sqrt{3}$+3；
②过点C的“蛋圆”切线交x轴于G，求G点的坐标；
（3）P点在线段OB上运动，过P作x轴的垂线，交抛物线于点E，交BD于点F，连结DE和BE后，是否存在这样的点E，使△BDE的面积最大？若存在，请求出点E的坐标和△BDE面积的最大值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网