题目内容
20. 如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )
如图,∠1=∠2,下列选项中不能证明△ABC∽△ADE的是( )| A. | ∠B=∠D | B. | ∠C=∠E | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ |
分析 根据∠1=∠2,可知∠DAE=∠BAC,因此只要再找一组角或夹这组角的一组对应边成比例即可.
解答 解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
A和B符合有两组角对应相等的两个三角形相似;
C、符合两组对应边的比相等且相应的夹角相等的两个三角形相似;
D、对应边成比例但无法证明其夹角相等,故其不能推出两三角形相似.
故选D.
点评 此题考查了相似三角形的判定:①有两个对应角相等的三角形相似;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.小红和小丽以大树为起点,小红向东走10米记作+10米,小丽向西走8米记作-8米,小红和小丽相距( )米.
| A. | 8米 | B. | 10米 | C. | 18米 | D. | 无法确定 |
9.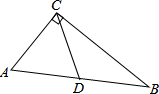 如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
 如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
10.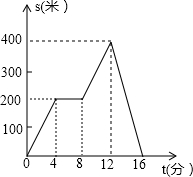 小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系.根据图象,下列信息错误的是( )
小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系.根据图象,下列信息错误的是( )
 小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系.根据图象,下列信息错误的是( )
小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系.根据图象,下列信息错误的是( )| A. | 小明看报用时8分钟 | B. | 公共阅报栏距小明家200米 | ||
| C. | 公共阅报栏距小明家200米 | D. | 小明从出发到回家共用时16分钟 |
 图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是4平方厘米.
图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是4平方厘米.