题目内容
14.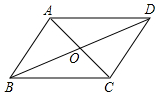 如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,平行四边形ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 26 | B. | 20 | C. | 17 | D. | 13 |
分析 由平行四边形的性质得出OA=OC=3,OB=OD=6,BC=AD=8,即可求出△OBC的周长.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17.
故选:C.
点评 本题主要考查了平行四边形的性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
2.对于不等式2x>-4,下列解集正确的是( )
| A. | x>2 | B. | x>-2 | C. | x<-2 | D. | x>-$\frac{1}{2}$ |
9.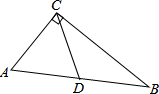 如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
 如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )
如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=2,则AB的长是( )| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
19.355、444、533的大小关系是( )
| A. | 355<444<533 | B. | 444<355<533 | C. | 533<444<355 | D. | 533<355<444 |
6.男生小明和三名女生、四名男生一起玩丢手帕游戏,小明随意将手帕丢在一名同学的后面,那么这名同学是女生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | 无法确定 |
3.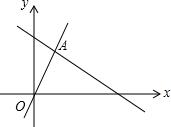 如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
 如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )| A. | x<$\frac{3}{2}$ | B. | x<3 | C. | x>$\frac{3}{2}$ | D. | x>3 |
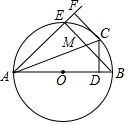 如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.
如图,AB为⊙O的直径,点C是⊙O上的一点,CD⊥AB,垂足为点D,CF⊥AF,且CF=CD,AF交⊙O于点E,BE交AC于点M.