题目内容
16.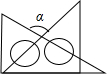 将一副三角板按如图所示摆放,图中∠α的度数是( )
将一副三角板按如图所示摆放,图中∠α的度数是( )| A. | 120° | B. | 105° | C. | 90° | D. | 75° |
分析 先根据直角三角形的性质得出∠BAE及∠E的度数,再由三角形内角和定理及对顶角的性质即可得出结论.
解答  解:∵图中是一副直角三角板,
解:∵图中是一副直角三角板,
∴∠BAE=45°,∠E=30°,
∴∠AFE=180°-∠BAE-∠E=105°,
∴∠α=105°.
故选B.
点评 本题考查的是三角形外角的性质,三角形内角和定理,即三角形内角和是180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.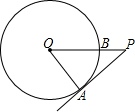 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=3,OA=4,则cos∠APO的值为( )
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=3,OA=4,则cos∠APO的值为( )
 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=3,OA=4,则cos∠APO的值为( )
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=3,OA=4,则cos∠APO的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
8. 有理数a、b、c在数轴上的位置如图所示,则a、b、c的大小关系是( )
有理数a、b、c在数轴上的位置如图所示,则a、b、c的大小关系是( )
 有理数a、b、c在数轴上的位置如图所示,则a、b、c的大小关系是( )
有理数a、b、c在数轴上的位置如图所示,则a、b、c的大小关系是( )| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c<a<b |
5.观察下面点阵图和相应的等式,探究其中的规律:

①1=12;②1+3=22;③1+3+5=32;④1+3+5+7=42;⑤1+3+5+7+9=52;…
按此规律1+3+5+7+…+(2n-1)=( )

①1=12;②1+3=22;③1+3+5=32;④1+3+5+7=42;⑤1+3+5+7+9=52;…
按此规律1+3+5+7+…+(2n-1)=( )
| A. | 2n2 | B. | n2 | C. | (2n-1)2 | D. | (n-1)2 |
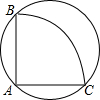 如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).
如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).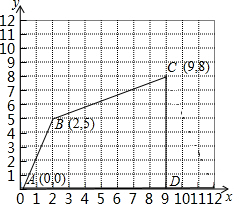 在如图所示的直角坐标系中,四边形ABCD的各个顶点的坐标分别是A(0,0)、B(2,5)、C(9,8)、D(9,0),求出这个四边形的面积.
在如图所示的直角坐标系中,四边形ABCD的各个顶点的坐标分别是A(0,0)、B(2,5)、C(9,8)、D(9,0),求出这个四边形的面积.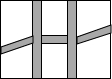 某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形)
某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形) 如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?
如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?