题目内容
7.已知点(-2,y1),(-3,y2)、(1,y3)在函数y=2x2+8x+7的图象上.则y1、y2、y3的大小关系是y3>y2>y1..分析 先求出二次函数y=2x2+8x+7的图象的对称轴,然后判断出A(-2,y1),B(-3,y2),C(1,y3)在抛物线上的位置,再求解.
解答 解:∵二次函数y=2x2+8x+7中a=2>0,
∴开口向上,对称轴为x=-2,
∵(-2,y1)中x=-2,y1最小,(1,y3),点B关于对称轴的对称点B′横坐标是2×(-2)-1=-5,则有B′(-5,y3),因为在对称轴得右侧,y随x得增大而增大,故y3>y2.
∴y3>y2>y1.
故答案为:y3>y2>y1.
点评 此题考查二次函数图象上点的坐标特征,关键是掌握二次函数图象的性质.

练习册系列答案
相关题目
17.下列方程一定是一元二次方程的是( )
| A. | (a2+1)x2+bx+c=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2+$\frac{2}{x}$-1=0 |
18.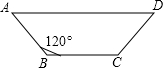 如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
 如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )| A. | $4\sqrt{3}{m^2}$ | B. | 9m2 | C. | 3m2 | D. | $\frac{{4\sqrt{3}}}{3}{m^2}$ |
15.使代数式$\frac{\sqrt{2x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≥-$\frac{1}{2}$且x≠1 | C. | x≥-$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$且x≠1 |
12.若3y-6x=0,则x:y等于( )
| A. | -2:1 | B. | 2:1 | C. | -1:2 | D. | 1:2 |
16.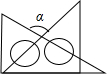 将一副三角板按如图所示摆放,图中∠α的度数是( )
将一副三角板按如图所示摆放,图中∠α的度数是( )
 将一副三角板按如图所示摆放,图中∠α的度数是( )
将一副三角板按如图所示摆放,图中∠α的度数是( )| A. | 120° | B. | 105° | C. | 90° | D. | 75° |
 如图所示是一住宅的建筑平面图(图中长度单位:m).用式子表示这所住宅的建筑面积是(x2+2x+18)m2.
如图所示是一住宅的建筑平面图(图中长度单位:m).用式子表示这所住宅的建筑面积是(x2+2x+18)m2.