题目内容
2.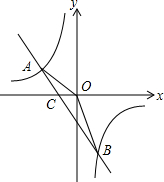 已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.(1)求反比例函数和一次函数的表达式;
(2)若直线AB交x轴于点C,求△AOB的面积.
分析 (1)把点($\frac{1}{3}$,-3)代入反比例函数y=$\frac{{k}_{1}}{3x}$的即可求出k1的值,进而求出反比例函数的解析式;再把点A的坐标代入反比例函数的关系式求出a的值,把A、B两点坐标代入一次函数的关系式即可求出一次函数的关系式;
(2)根据(1)中求出的一次函数的关系式求出点C的坐标,再根据S△ABO=S△AOC+S△BOC进行解答;
解答 解:(1)∵反比例函数y=$\frac{{k}_{1}}{3x}$过B($\frac{1}{3}$,-3),
∴-3=$\frac{{k}_{1}}{1}$,即k1=-3,
∴此反比例函数的解析式为:y=-$\frac{1}{x}$;
∵反比例函数y=$\frac{{k}_{1}}{3x}$过A(-1,a),
∴a=-$\frac{1}{-1}$=1;
∵一次函数y=k2x+m的图象交于两点A(-1,1),B($\frac{1}{3}$,-3).
∴$\left\{\begin{array}{l}{-{k}_{2}+m=1}\\{\frac{1}{3}{k}_{2}+m=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{2}=-3}\\{m=-2}\end{array}\right.$.
∴一次函数y=k2x+m的解析式为:y=-3x-2;
(2)∵直线AB的解析式为y=-3x-2,
∴C(-$\frac{2}{3}$,0),
∴OC=$\frac{2}{3}$,
∵A(-1,1),B($\frac{1}{3}$,-3),
∴S△ABO=S△AOC+S△BOC=$\frac{1}{2}$×$\frac{2}{3}$×1+$\frac{1}{2}$×$\frac{2}{3}$×3=$\frac{1}{3}$+1=1$\frac{1}{3}$.
故△AOB的面积是1$\frac{1}{3}$.
点评 本题考查的是反比例函数与一次函数的交点问题及用待定系数法求一次函数及反比例函数的关系式,在解(2)时能根据S△ABO=S△AOC+S△BOC求解是解答此题的关键.

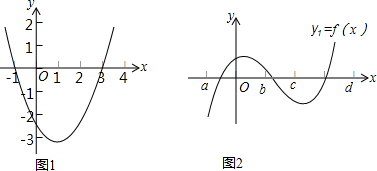
 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )| A. | 函数值y随x的增大而减少 | B. | kb<0 | ||
| C. | 当x<1时,y>0 | D. | k+b<0 |
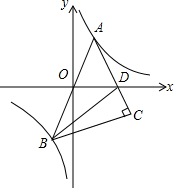 如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )
如图,点A在反比例函数y=$\frac{6}{x}$图象第一象限的分支上,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,若△OAD与△BCD的面积相等,则点A的横坐标是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
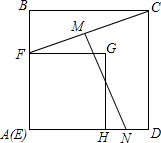 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )| A. | $\frac{25}{4}$cm | B. | $\frac{73}{4}$cm | C. | $\frac{\sqrt{73}}{2}$cm | D. | $\frac{\sqrt{75}}{2}$cm |
| A. | a3+a3=26a | B. | 3a-2a=a | C. | 3a2b-4b2a=-a2b | D. | (-a)2=-a2 |
| A. | x<1 | B. | x≤1 | C. | x>1 | D. | x≥1 |
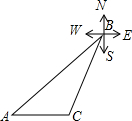 如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)
如图,某海洋区域内有A、B两个小岛,其中A岛在B岛的西南方向,一天,一只轮船上午8时从A岛出发,沿正东方向以每小时80海里的速度航行1.5小时到达C处,此时轮船在B岛的南偏西15°方向,试求A、B两岛相距多少海里?(结果保留根号)(注:E-东方,W-西方,S-南方,N-北方)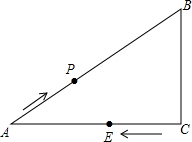 如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?