题目内容
以半圆的直径为一边作等边三角形,求半圆周被这个三角形其他两边截成的二条弧所对的圆心角的度数.
考点:圆周角定理,等边三角形的性质
专题:
分析:首先根据题意画出图形,连接DO,EO.由同圆的半径相等得出BO=DO=EO=CO,根据等边对等角得到∠B=∠ODB,∠C=∠OEC,而根据等边三角形的性质有∠B=∠C=60°,于是∠ODB=∠B=60°,∠OEC=∠C=60°,那么△BOD等边三角形,△CEO为等边三角形,根据等边三角形的性质求出∠BOD=∠COE=60°,根据平角的定义得到∠DOE=180°-60°-60°=60°.
解答: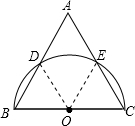 解:如图,已知BC为半圆O的直径,△ABC是等边三角形,AB交半圆上的点为D,AC交半圆上的点为E,连接DO,EO.
解:如图,已知BC为半圆O的直径,△ABC是等边三角形,AB交半圆上的点为D,AC交半圆上的点为E,连接DO,EO.
∵BO=DO=EO=CO,
∴∠B=∠ODB,∠C=∠OEC,
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∴∠ODB=∠B=60°,∠OEC=∠C=60°,
∴△BOD等边三角形,△CEO为等边三角形,
∴∠BOD=∠COE=60°,∠DOE=180°-60°-60°=60°.
 解:如图,已知BC为半圆O的直径,△ABC是等边三角形,AB交半圆上的点为D,AC交半圆上的点为E,连接DO,EO.
解:如图,已知BC为半圆O的直径,△ABC是等边三角形,AB交半圆上的点为D,AC交半圆上的点为E,连接DO,EO.∵BO=DO=EO=CO,
∴∠B=∠ODB,∠C=∠OEC,
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∴∠ODB=∠B=60°,∠OEC=∠C=60°,
∴△BOD等边三角形,△CEO为等边三角形,
∴∠BOD=∠COE=60°,∠DOE=180°-60°-60°=60°.
点评:本题考查了等腰三角形的性质,等边三角形的判定与性质,平角的定义,准确画出图形是解题的关键.

练习册系列答案
相关题目
一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5t2+10t+1,则小球距离地面的最大高度是( )
| A、1米 | B、5米 | C、6米 | D、7米 |
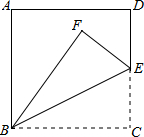 在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数为( )
在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数为( )| A、15° | B、20° |
| C、25° | D、30° |
 已知,∠DAB=∠CAE,AD=2,AC=6,AE=4,AB=3,DE=5,求BC长.
已知,∠DAB=∠CAE,AD=2,AC=6,AE=4,AB=3,DE=5,求BC长. 如图,△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点D.若AC+BC=10cm,则△DBC的周长为
如图,△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点D.若AC+BC=10cm,则△DBC的周长为 如图,∠AOE=90°,OD、OB分别是∠EOC、∠AOC的角平分线,那么不大于90°的角有
如图,∠AOE=90°,OD、OB分别是∠EOC、∠AOC的角平分线,那么不大于90°的角有 如图所示,梯形ABCD中,AB∥DC.AD=BC=DC=2,AC⊥BC,求AB,AC的长.
如图所示,梯形ABCD中,AB∥DC.AD=BC=DC=2,AC⊥BC,求AB,AC的长.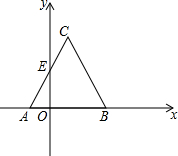 如图所示的平面直角坐标系,在△ABC中,∠A=60°,边AB在x轴上,AC交y轴于点E,AC、BC的长是关于x的方程x2-16x+64=0的两个根,且OA:OB=1:3.
如图所示的平面直角坐标系,在△ABC中,∠A=60°,边AB在x轴上,AC交y轴于点E,AC、BC的长是关于x的方程x2-16x+64=0的两个根,且OA:OB=1:3.