题目内容
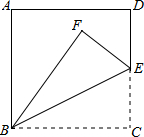在正方形ABCD中，E为DC边上的一点，沿线段BE对折后，若∠ABF比∠EBF大15°，则∠EBF的度数为（ ）| A、15° | B、20° |
| C、25° | D、30° |
考点：角的计算,翻折变换（折叠问题）
专题：
分析：根据折叠角相等和正方形各内角为直角的性质即可求得∠EBF的度数．
解答：解：∵∠FBE是∠CBE折叠形成，
∴∠FBE=∠CBE，
∵∠ABF-∠EBF=15°，∠ABF+∠EBF+∠CBE=90°，
∴∠EBF=25°，
故选：C．
∴∠FBE=∠CBE，
∵∠ABF-∠EBF=15°，∠ABF+∠EBF+∠CBE=90°，
∴∠EBF=25°，
故选：C．
点评：本题考查了折叠的性质，考查了正方形各内角为直角的性质，本题中求得∠FBE=∠CBE是解题的关键．
练习册系列答案
相关题目
如图所示，OC是⊙O的半径，A是圆上一点，延长OC到点B，使OC=BC，且AC=BC，求证：AB为⊙O的切线．
如图，小明沿着某斜坡向上行走了13m后，他的相对位置升高了5m，如果他沿着该斜坡行走了26米，那么他的相对位置升高了
如图，下列说法中错误的是（ ）| A、∠3和∠5是同位角 |
| B、∠4和∠5是同旁内角 |
| C、∠2和∠4是对顶角 |
| D、∠1和∠4是内错角 |