题目内容
17.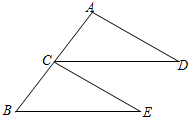 已知:如图,CD=BE,CD∥BE,∠D=∠E.求证:点C是线段AB的中点.
已知:如图,CD=BE,CD∥BE,∠D=∠E.求证:点C是线段AB的中点.
分析 由CD与BE平行,利用两直线平行同位角相等得到一对角相等,利用ASA得到三角形ACD与三角形CBE全等,利用全等三角形对应边相等得到AC=BC,即可得证.
解答 证明:∵CD∥BE,
∴∠ACD=∠B,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ACD=∠B}\\{CD=BE}\\{∠D=∠E}\end{array}\right.$,
∴△ACD≌△CBE(ASA),
∴AC=BC,
则点C是线段AB的中点.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,甲乙两船从港口A同时出发,甲船以12海里/时速度向东北方向航行,乙船以16海里/时速度向东南方向航行,2小时后,两船相距多少海里?
如图,甲乙两船从港口A同时出发,甲船以12海里/时速度向东北方向航行,乙船以16海里/时速度向东南方向航行,2小时后,两船相距多少海里?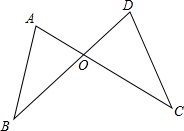 如图,已知AB,CD相交于点O,且AB=DC,AC=DB,∠A=65°,∠ACD=45°.
如图,已知AB,CD相交于点O,且AB=DC,AC=DB,∠A=65°,∠ACD=45°.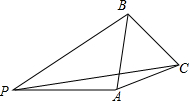 如图,P是等边三角形ABC外一点,PA=3,PB=4,PC=5,求∠BPA的度数.
如图,P是等边三角形ABC外一点,PA=3,PB=4,PC=5,求∠BPA的度数.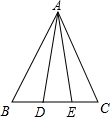 如图,点D、E在BC上,AB=AC,AD=AE.求证:∠BAD=∠CAE.
如图,点D、E在BC上,AB=AC,AD=AE.求证:∠BAD=∠CAE.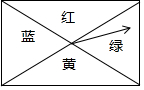 如图,一块长宽不等的矩形木板,连接对角线后被分成4个区域,分别涂上红、黄、蓝、绿四色,木板中间装有指针,指针转动停止后,下面两个结论:
如图,一块长宽不等的矩形木板,连接对角线后被分成4个区域,分别涂上红、黄、蓝、绿四色,木板中间装有指针,指针转动停止后,下面两个结论: