题目内容
16. 如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.
如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.(1)求证:BC∥DE;
(2)若BC:DF=4:3,求tan∠ABC的值.
分析 (1)连接OF,由题意,可得∠BOF=∠COF=90°,根据切线的性质,可得∠OFE=90°,利用平行线的判定,即可证明;
(2)过点B作BG⊥DE于点G,可得四边形BGFO是正方形,由BC:DF=4:3,可得BG:DG=2:1,利用锐角三角函数即可求得tan∠ABC.
解答 解:(1)连接OF,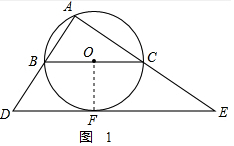
∵点F为$\widehat{BC}$的中点,
∴$\widehat{BF}=\widehat{CF}$,
∴∠BOF=∠COF,
∵BC为直径,
∴∠BOF+∠COF=180°,
∴∠BOF=∠COF=90°,
∵过F点的切线交于D、E两点,
∴OF⊥DE,
∴∠OFE=90°,
∴∠BOF=∠OFE,
∴BC∥DE;
(2)过点B作BG⊥DE于点G,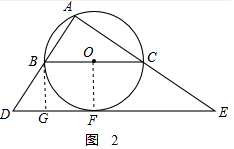
∴四边形BGFO是正方形,
∴BG=OF=GF=OB,
∵BC:DF=4:3,
∴BG:DG=2:1,
由(1)可知,tan∠ABC=tan∠BDG=$\frac{BG}{DG}$=2.
点评 本题主要考查切线的性质及解直角三角形,解决第(1)题,需要灵活运用切线的性质及平行线的性质和判定定理,(2)题能根据BC:DF=4:3,得到BG:DG=2:1是解题的关键.

练习册系列答案
相关题目
4.将正整数依次按如表规律排成四列,请根据表中的排列规律回答下列问题:
(1)第6行第2列的数是多少?
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
11. 如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
 如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )
如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )| A. | 5对 | B. | 6对 | C. | 8对 | D. | 10对 |
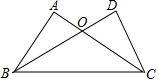 如图,AC、BD相交于点O,AB=CD,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是∠A=∠D.
如图,AC、BD相交于点O,AB=CD,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是∠A=∠D.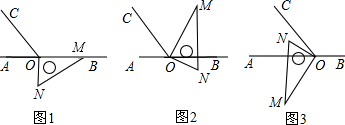
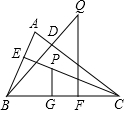 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC. 如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.求证△ACD∽△EGH.
如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.求证△ACD∽△EGH.