题目内容
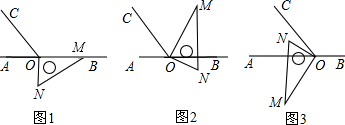
7.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角形的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少秒?(直接写出结果)
分析 (1)根据平角的定义求出∠AOC,根据角平分线的定义计算即可;
(2)根据(1)的结论和旋转的性质解答.
解答 解:(1)直线ON平分∠AOC,
∵∠BOC=120°,
∴∠AOC=60°,
∵OM平分∠BOC,
∴∠BOM=$\frac{1}{2}$∠BOC=60°,
∵∠MON=90°,
∴∠BON=30°,
∴直线ON平分∠AOC;
(2)由(1)得,当直线ON旋转60°或240°时,ON平分锐角∠AOC,
∴t=10或40秒.
点评 本题考查的是角的计算、角平分线的定义,掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
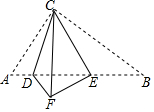 如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.
如图,在△ACB中,∠ACB=90°,∠A=45°,沿图中CD翻折,将△ACD折到△FCD,然后沿CE将△CEB翻折,使CB与CF重合,观察这个图形.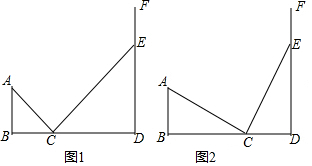

 如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.
如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.